某種落地燈如圖1所示，AB為立桿，其高為84cm；BC為支桿，它可繞點B旋轉，其中BC長為54cm；DE為懸桿，滑動懸桿可調節CD的長度．支桿BC與懸桿DE之間的夾角∠BCD為60°．
（1）如圖2，當支桿BC與地面垂直，且CD的長為50cm時，求燈泡懸掛點D距離地面的高度；
（2）在圖2所示的狀態下，將支桿BC繞點B順時針旋轉20°，同時調節CD的長（如圖3），此時測得燈泡懸掛點D到地面的距離為90cm,求CD的長．（結果精確到1cm,參考數據：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）
【考點】解直角三角形的應用．
【答案】（1）113cm；
（2）CD的長為58cm．
（2）CD的長為58cm．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/21 14:0:2組卷：2519引用：10難度：0.6
相似題
-
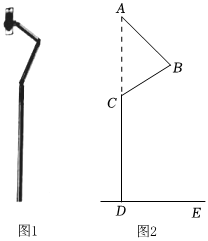1．如圖1是一臺多功能手機支架，圖2是其側面示意圖，DE為地面，支架CD垂直地面，AB，BC可分別繞點B，C轉動，測量知BC=30cm,CD=100cm.當AB，BC轉動到∠ABC=75°，∠BCD=120°，且A、C、D三點共線時，求點A到地面的距離．發布：2025/5/29 16:30:1組卷：269引用：2難度：0.5 -
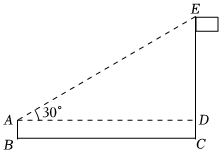2．如圖，小明利用一個銳角是30°的三角板測量操場旗桿的高度，已知他與旗桿之間的水平距離BC為15m,AB為1.5m（即小明的眼睛與地面的距離），那么旗桿的高度是 ．發布：2025/5/29 16:30:1組卷：63引用：2難度：0.8 -
3．湘潭縣石鼓油紙傘因古老工藝和文化底蘊，已成為石鼓鄉村旅游的一張靚麗名片．某中學八年級數學興趣小組參觀后，進行了設計傘的實踐活動．小文依據黃金分割的美學設計理念，設計了中截面如圖所示的傘骨結構（其中
≈0.618）：傘柄AH始終平分∠BAC，AB=AC=20cm,當∠BAC=120°時，傘完全打開，此時∠BDC=90°．請問最少需要準備多長的傘柄？（結果保留整數，參考數據：DHAH≈1.732）3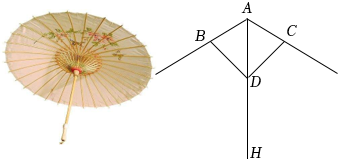
發布：2025/5/29 17:0:2組卷：767引用：3難度：0.5