在四邊形ABCD中，AD∥BC，∠BAD=∠D=60°，AD=12，CD=8，過點C作CE⊥AD于點E，連接BE，且∠CBE=∠D，將半圓O的直徑PQ放在邊AD上，且點P與點A重合，PQ=6，將半圓O繞點A順時針旋轉α（0°≤α≤90°），如圖1所示．
（1）求證：△CDE≌△EBC；
（2）在旋轉過程中，當點O與BE的距離最短時，求α的度數；
（3）當α=90°時，點H從點Q開始沿?PQ以每秒π4個單位長的速度運動，同時半圓O從點A出發沿AD方向以每秒1個單位長的速度向右平移，運動時間為t秒（0≤t≤12）．
①如圖2，當半圓O與BE相切于點K時，求?HQ的長；
②當?PQ（包括端點）與四邊形BCDE的邊有兩個交點時，請直接寫出t的取值范圍．
?
PQ
π
4
?
HQ
?
PQ
【考點】圓的綜合題．
【答案】（1）證明見解析；（2）30°；（3）①π；②t的取值范圍為：8-3＜t≤8-2或t=12-3或12-2＜t＜12．
8
-
3
3
4
3
3
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/26 11:36:51組卷：137引用：1難度：0.4
相似題
-
1．等腰三角形AFG中AF=AG，且內接于圓O，D、E為邊FG上兩點（D在F、E之間），分別延長AD、AE交圓O于B、C兩點（如圖1），記∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）連接CF，交AB于H（如圖2）．若β=45°，且BC×EF=AE×CF．求證：∠AHC=2∠BAC；
（3）在（2）的條件下，取CH中點M，連接OM、GM（如圖3），若∠OGM=2α-45°，
①求證：GM∥BC，GM=BC；12
②請直接寫出的值．OMMC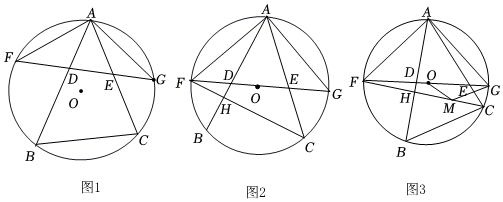
發布：2025/6/7 16:0:2組卷：1490引用：8難度：0.1 -
2．已知，線段AB是⊙O的直徑，弦CD⊥AB于點H，點M是優弧CBD上的任意一點，AH=2，CH=4．
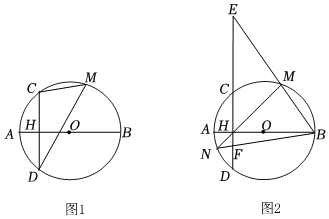
（1）如圖1，
①求⊙O的半徑；
②求sin∠CMD的值．
（2）如圖2，直線BM交直線CD于點E，直線MH交⊙O于點N，連結BN交CD于點F，求HE?FH的值．發布：2025/6/7 7:0:1組卷：476引用：2難度：0.3 -
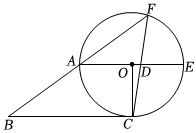3．如圖，四邊形OABC中，AO∥BC，∠AOC=90°，AO=3，AB=5．以O為圓心，OA為半徑作圓，⊙O經過點C，且與BA的延長線交于F．延長AO交圓于E，連接FC交AE于點D．
（1）求證：BC是⊙O的切線；
（2）求cos∠FAE的值；
（3）求線段OD的長．發布：2025/6/7 5:0:1組卷：79引用：1難度：0.3