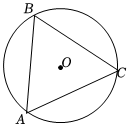
如圖，△ABC內接于⊙O（∠ACB＞90°），連接OA，OC，記∠BAC=α，∠BCO=β，∠BAO=γ．
（1）證明：α+β=90°；
（2）設OC與AB交于點D，⊙O半徑為2，
①若β=γ+45°，AD=2OD，求由線段BD，CD，弧BC圍成的圖形面積S；
②若α+2γ=90°，設sinα=k,用含k的代數式表示線段OD的長．
【答案】（1）證明見解答過程；
（2）①；
②．
（2）①
π
-
3
12
②
2
2
k
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：597引用：6難度：0.3
