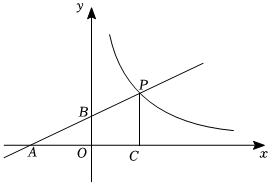
如圖，直線y=ax+2與x軸、y軸分別相交于A、B兩點(diǎn)，與雙曲線y=kx（x＞0）相交于點(diǎn)P，PC⊥x軸于點(diǎn)C，且PC=4，點(diǎn)A的坐標(biāo)為（-4，0）．
（1）求一次函數(shù)的解析式；
（2）求雙曲線的解析式；
（3）若點(diǎn)Q為雙曲線上點(diǎn)P右側(cè)的一點(diǎn)，且QH⊥x軸于H，當(dāng)以點(diǎn)Q、C、H為頂點(diǎn)的三角形與△AOB相似時(shí)，求點(diǎn)Q的橫坐標(biāo)．
y
=
k
x
（
x
＞
0
）
【考點(diǎn)】反比例函數(shù)綜合題．
【答案】（1）y=x+2；
（2）y=；
（3）Q（8，2）或Q（2+2，4-4）．
1
2
（2）y=
16
x
（3）Q（8，2）或Q（2+2
3
3
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/2 15:0:1組卷：148引用：1難度：0.2
相似題
-
1．如圖1，平面直角坐標(biāo)系中，點(diǎn)B的坐標(biāo)是（5，4），過(guò)B作BC⊥x軸于C，BA⊥y軸于A，點(diǎn)P從點(diǎn)A出發(fā)，以每秒1個(gè)單位長(zhǎng)度的速度沿A→B運(yùn)動(dòng)，在點(diǎn)P運(yùn)動(dòng)過(guò)程中，函數(shù)
（k≠0）的圖象在第一象限內(nèi)的一支雙曲線經(jīng)過(guò)點(diǎn)P，且與線段BC交于M點(diǎn)，連接PM、AC，設(shè)運(yùn)動(dòng)時(shí)間為t（0＜t＜5）秒．y=kx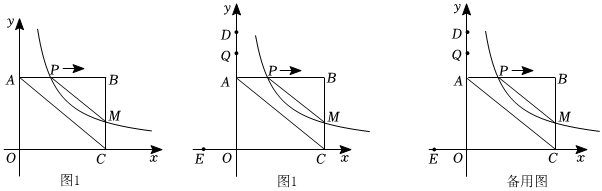
?
（1）點(diǎn)P的坐標(biāo)為 ，線段BM的長(zhǎng)度為 ．（用含有t的式子表示）
（2）判斷PM與AC的位置關(guān)系，并證明；
（3）已知點(diǎn)D的坐標(biāo)是（0，8），點(diǎn)E的坐標(biāo)為（-2，0），動(dòng)點(diǎn)Q從點(diǎn)D出發(fā)，與點(diǎn)P同時(shí)出發(fā)，以每秒2個(gè)單位長(zhǎng)度的速度沿D→O→E方向運(yùn)動(dòng)，在點(diǎn)P、點(diǎn)Q的運(yùn)動(dòng)過(guò)程中，坐標(biāo)軸上是否存在點(diǎn)N，使得以P、Q、M、N為頂點(diǎn)的四邊形是平行四邊形，若存在，求出點(diǎn)N的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．發(fā)布：2025/6/4 3:30:2組卷：866引用：1難度：0.2 -
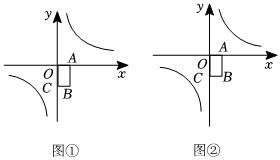2．如圖，反比例函數(shù)y=，矩形OABC的頂點(diǎn)B的坐標(biāo)為（1，-2），僅用無(wú)刻度直尺，按下列要求作圖．3x
（1）在圖①中，找到點(diǎn)E（1，3），并作出點(diǎn)E關(guān)于原點(diǎn)的對(duì)稱點(diǎn)F．
（2）在（1）的前提下，在圖②中，在反比例圖象上找到點(diǎn)G，點(diǎn)H，使得點(diǎn)E，F(xiàn)，G，H構(gòu)成的四邊形正好為矩形．發(fā)布：2025/6/3 18:30:1組卷：33引用：1難度：0.1 -
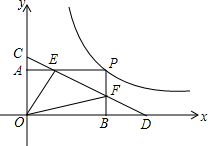3．如圖．矩形OAPB的頂點(diǎn)P在反比例函數(shù)y=（k＞0，x＞0）的圖象上，點(diǎn)E、F分別是矩形的邊PA，PB上的動(dòng)點(diǎn)，直線EF分別交y軸、x軸于C，D兩點(diǎn)．現(xiàn)給出如下命題：①若點(diǎn)E、F恰同在反比例函數(shù)y=kx（k＞m＞0）的圖象上，則S四邊形OEPF=k-m；②△ACE≌△BFD；③若OC=OD=mx，則△OCF∽△EOF；④CE+DF=EF．其中結(jié)論正確的是（ ）2k發(fā)布：2025/6/3 3:0:2組卷：552引用：3難度：0.3