秦九韶（1208年-1268年），字道古，漢族，生于普州安岳（今四川省安岳縣）人，祖籍魯郡（今河南范縣）．南宋著名數(shù)學(xué)家，與李冶、楊輝、朱世杰并稱宋元數(shù)學(xué)四大家．他精研星象、音律、算術(shù)、詩(shī)詞、弓劍、營(yíng)造之學(xué)，是一位既重視理論又重視實(shí)踐，既善于繼承又勇于創(chuàng)新的世界著名數(shù)學(xué)家．他所提出的大衍求一術(shù)（中國(guó)剩余定理）和正負(fù)開方術(shù)及其名著《數(shù)書九章》，是中國(guó)數(shù)學(xué)史、乃至世界數(shù)學(xué)史上光彩奪目的一頁(yè)，對(duì)后世數(shù)學(xué)發(fā)展產(chǎn)生了廣泛的影響．他寫的《數(shù)書九章》序堪稱一篇奇文．秦九韶的數(shù)學(xué)成果豐碩，其中關(guān)于三角形的面積公式與古希臘幾何學(xué)家海倫的成果統(tǒng)稱海倫-秦九韶公式．如果一個(gè)三角形的三邊長(zhǎng)分別是a、b、c,記p=a+b+c2，那么三角形的面積為：s=p（p-a）（p-b）（p-c）．
（1）在△ABC中，BC=4，AC=AB=3，請(qǐng)用上面的公式計(jì)算△ABC的面積．
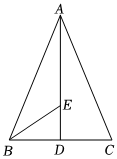
（2）如圖，在△ABC中，BC=6，AC=AB=7，AD⊥BC，垂足為D，∠ABC的平分線交AD于點(diǎn)E．求BE的長(zhǎng)．
a
+
b
+
c
2
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
【考點(diǎn)】二次根式的應(yīng)用；等腰三角形的性質(zhì)．
【答案】（1）；
（2）．
2
5
（2）
3
5
35
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：67引用：2難度：0.6
相似題
-
1．在《九章算術(shù)》中有求三角形面積的公式“底乘高的一半”，但是在實(shí)際丈量土地面積時(shí)，準(zhǔn)確測(cè)量高并不容易，所以古人想到了能否利用三角形的三條邊長(zhǎng)來(lái)求面積．我國(guó)南宋著名的數(shù)學(xué)家秦九韶（約1202～約1261）提出了“三斜求積術(shù)”，簡(jiǎn)稱秦九韶公式．古希臘的幾何學(xué)家海倫（Heron,約公元50年）在數(shù)學(xué)史上以解決幾何測(cè)量問題而聞名．在他的著作《度量》一書中，給出了利用三角形三邊長(zhǎng)求面積的方法和證明，相傳這個(gè)公式最早是由古希臘數(shù)學(xué)家阿基米德（公元前287年—公元前212年）得出的．在我國(guó)稱這個(gè)公式為海倫—秦九韶公式．它的表述為：如果一個(gè)三角形三邊長(zhǎng)分別為a、b、c,那么三角形的面積為
．（公式里的p為半周長(zhǎng)，即S=p（p-a）（p-b）（p-c））p=a+b+c2
請(qǐng)利用海倫——秦九韶公式解決以下問題：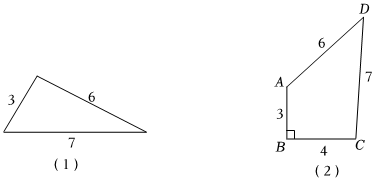
（1）三邊長(zhǎng)分別為3、6、7的三角形面積為 ．
（2）四邊形ABCD中，AB=3，BC=4，CD=7，AD=6，∠B=90°，求該四邊形的面積．發(fā)布：2025/6/8 2:30:2組卷：170引用：2難度：0.6 -
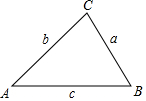2．古希臘幾何學(xué)家海倫和我國(guó)宋代數(shù)學(xué)家秦九韶都曾提出利用三角形的三邊求面積的公式，稱為海倫-秦九韶公式：如果一個(gè)三角形的三邊長(zhǎng)分別是a,b,c,記p=，那么三角形的面積為S=a+b+c2．如圖，在△ABC中，∠A，∠B，∠C所對(duì)的邊分別記為a,b,c,若a=5，b=6，c=7，則△ABC的面積為（ ）p（p-a）（p-b）（p-c）發(fā)布：2025/6/8 3:30:1組卷：1604引用：23難度：0.8 -
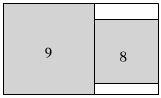3．如圖在一長(zhǎng)方形中無(wú)重疊地放入面積分別為9和8的兩張正方形紙片，則圖中空白部分的面積為 ．發(fā)布：2025/6/8 7:30:1組卷：64引用：2難度：0.6