甲、乙、丙三位同學(xué)進(jìn)行立定跳遠(yuǎn)比賽，每人輪流跳一次稱為一輪，每輪按名次從高到低分別得3分、2分、1分（沒(méi)有并列名次）．他們一共進(jìn)行了五輪比賽，結(jié)果甲共得14分；乙第一輪得3分，第二輪得1分，且總分最低．那么丙得到的分?jǐn)?shù)是
9分
9分
．

【答案】9分

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/5/28 5:0:1組卷：219引用：4難度：0.5

相似題

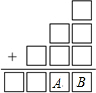1．在右邊的加法算式中，每一個(gè)□表示一個(gè)數(shù)字，任意兩個(gè)數(shù)字都不相同，那么A與B乘積的最大值是

．
發(fā)布：2025/5/28 16:0:1組卷：41引用：1難度：0.5
解析
2．x,y為正整數(shù)，且兩個(gè)分?jǐn)?shù)之和
x
2
-
1
y
+
1
+
y
2
-
1
x
+
1
也是整數(shù)，求證：這兩個(gè)分?jǐn)?shù)都是整數(shù)．
發(fā)布：2025/5/28 16:0:1組卷：66引用：1難度：0.1
解析
3．已知下面等式對(duì)任意實(shí)數(shù)x都成立（n為正整數(shù)）：（1+x）+（1+x）²+（1+x）³+…+（1+x）ⁿ=a₀+a₁x+a₂x²+…+a_nxⁿ，且a₁+a₂+a₃+…+a_n=57，則滿足條件的n的可能值是

．
發(fā)布：2025/5/28 16:30:2組卷：78引用：2難度：0.5
解析

相關(guān)試卷

1．在右邊的加法算式中，每一個(gè)□表示一個(gè)數(shù)字，任意兩個(gè)數(shù)字都不相同，那么A與B乘積的最大值是 ．