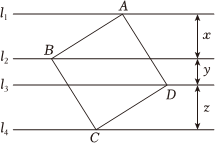
如圖，正方形ABCD的四個頂點分別在四條平行線l1、l2、l3、l4上，這四條直線中相鄰兩條之間的距離依次為x、y、z（x＞0，y＞0，z＞0）．
（1）求證：x=z；
（2）設正方形ABCD的面積為S．求證：S=（y+z）2+x2；
（3）若32x+y=1，當x變化時，試說明正方形ABCD的面積S隨x的變化情況．
3
2
【答案】（1）證明見解析；（2）證明見解析；（3）當x=時，S取得最小值；當＜x＜時，S隨x的增大而增大．
2
5
4
5
2
5
2
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/25 0:0:1組卷：8引用：1難度：0.5
相似題
-
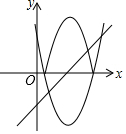1．課堂上，老師給出一道題：如圖，將拋物線C：y=x2-6x+5在x軸下方的圖象沿x軸翻折，翻折后得到的圖象與拋物線C在x軸上方的圖象記為G（包含x軸上的點），已知直線l：y=x+m與圖象G有兩個公共點，求m的取值范圍．甲同學的結果是-5＜m＜-1，乙同學的結果是m＞．下列說法正確的是（ ）54發布：2025/5/22 4:0:7組卷：839引用：4難度：0.7 -
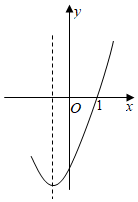2．已知關于x的一元二次方程x2+x-m=0．
（1）若方程有兩個不相等的實數根，求m的取值范圍；
（2）二次函數y=x2+x-m的部分圖象如圖所示，求一元二次方程x2+x-m=0的解．發布：2025/5/22 4:0:7組卷：2985引用：25難度：0.8 -
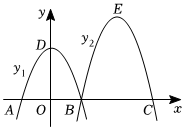3．如圖，拋物線y1截得坐標軸上的線段長AB=OD=6，D為y1的頂點，拋物線y2由y1平移得到，y2截得x軸上的線段長BC=9．若過原點的直線被拋物線y1，y2所截得的線段長相等，則這條直線的解析式為 ．發布：2025/5/22 2:30:1組卷：118引用：3難度：0.5