如圖1，非直徑的弦AB，CD在⊙O上運動，連接OA，OB，OC，OD．
（1）如圖2，當點B，D重合時，若∠AOB=100°，∠COD=40°，則∠ABC=30°30°．
（2）如圖3，當弦CD在弦AB所對的優弧上時，延長AD，BC交于點P，AB=4，CD=3，∠P=30°．
①∠AOB-∠COD是否為定值？若是，求出該值，否則說明理由；
②求⊙O半徑．
（3）如圖4，在（2）條件下，連接AC，直接寫出S△ACP的最大值．
CD
=
3
【考點】圓的綜合題．
【答案】30°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/22 0:0:8組卷：310引用：2難度：0.1
相似題
-
1．如圖，⊙O的半徑為5，弦BC=6，A為BC所對優弧上一動點，△ABC的外角平分線AP交⊙O于點P，直線AP與直線BC交于點E．
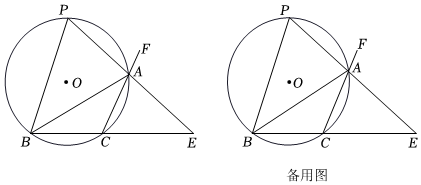
（1）求證：P為優弧BAC的中點；
（2）連接PC，求PC的長度；
（3）求sin∠BAC的值；
（4）若△ABC為非銳角三角形，請直接寫出△ABC的面積的最大值．發布：2025/6/15 3:0:1組卷：97引用：1難度：0.1 -
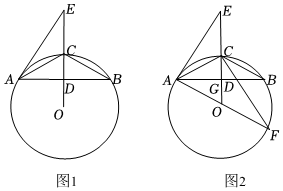2．如圖，⊙O為△ABC的外接圓，AC=BC，D為OC與AB的交點，E為線段OC延長線上一點，且∠EAC=∠ABC．
（1）求證：直線AE是⊙O的切線．
（2）若CD=6，AB=16，求⊙O的半徑；
（3）在（2）的基礎上，點F在⊙O上，且=?BC，△ACF的內心點G在AB邊上，求BG的長．?BF發布：2025/6/14 23:0:1組卷：1104引用：7難度：0.1 -
3．請閱讀下面材料，并完成相應的任務；
阿基米德折弦定理
阿基米德（Archimedes,公元前287-公元前212年，古希臘）是有史以來最偉大的數學家之一，他與牛頓、高斯并稱為三大數學王子．
阿拉伯Al-Biruni（973年-1050年）的譯文中保存了阿基米德折弦定理的內容，蘇聯在1964年根據Al-Biruni譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德的折弦定理．
阿基米德折弦定理：如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），BC＞AB，M是的中點，則從點M向BC所作垂線的垂足D是折弦ABC的中點，即CD=AB+BD．?ABC
這個定理有很多證明方法，下面是運用“垂線法”證明CD=AB+BD的部分證明過程．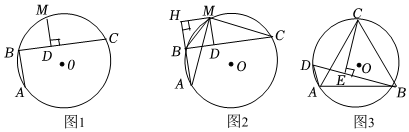
證明：如圖2，過點M作MH⊥射線AB，垂足為點H，連接MA，MB，MC．
∵M是的中點，?ABC
∴MA=MC．
…
任務：
（1）請按照上面的證明思路，寫出該證明的剩余部分；
（2）如圖3，已知等邊三角形ABC內接于⊙O，D為上一點，∠ABD=15°，CE⊥BD于點E，CE=2，連接AD，則△DAB的周長是 ．?AC發布：2025/6/15 17:30:2組卷：757引用：4難度：0.1