【問題提出】
如果從1,2,3……m,m個連續的自然數中選擇n個連續的自然數(n≤m),有多少種不同的選擇方法?
【問題探究】
為發現規律,我們采用一般問題特殊化的策略,先從最簡單的問題入手,再逐次遞進,最后得出一般性的結論
探究一:
如果從1,2,3……m,m個連續的自然數中選擇2個連續的自然數,會有多少種不同的選擇方法?
如圖1,當m=3,n=2時,顯然有2種不同的選擇方法;
如圖2,當m=4,n=2時,有1,2;2,3;3,4這3種不同的選擇方法;
如圖3,當m=5,n=2時,有 44種不同的選擇方法;
……
由上可知:從m個連續的自然數中選擇2個連續的自然數,有 m-1m-1種不同的選擇方法.
探究二:
如果從1,2,3……100,100個連續的自然數中選擇3個,4個……n(n≤100)個連續的自然數,分別有多少種不同的選擇方法?
我們借助下面的框圖繼續探究,發現規律并應用規律完成填空
| 1 | 2 | 3 | … | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
98
98
種不同的選擇方法;從100個連續的自然數中選擇4個連續的自然數,有
97
97
種不同的選擇方法;……
從100個連續的自然數中選擇8個連續的自然數,有
93
93
種不同的選擇方法;……
由上可知:如果從1,2,3……100,100個連續的自然數中選擇n(n≤100)個連續的自然數,有
(100-n+1)
(100-n+1)
種不同的選擇方法.【問題解決】
如果從1,2,3……m,m個連續的自然數中選擇n個連續的自然數(n≤m),有
(m-n+1)
(m-n+1)
種不同的選擇方法.【實際應用】
我們運用上面探究得到的結論,可以解決生活中的一些實際問題.
(1)今年國慶七天長假期間,小亮想參加某旅行社組織的青島兩日游,在出行日期上,他共有
6
6
種不同的選擇.(2)星期天,小明、小強和小華三個好朋友去電影院觀看《我和我的祖國》,售票員李阿姨為他們提供了第七排3號到15號的電影票讓他們選擇,如果他們想拿三張連號票,則一共有
11
11
種不同的選擇方法.【拓展延伸】
如圖4,將一個2×2的圖案放置在8×6的方格紙中,使它恰好蓋住其中的四個小正方形,共有
35
35
種不同的放置方法.
【考點】規律型:圖形的變化類.
【答案】4;m-1;98;97;93;(100-n+1);(m-n+1);6;11;35
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/5 8:0:8組卷:443引用:2難度:0.1
相似題
-
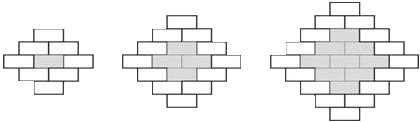
1.為美化市容,某廣場要在人行雨道上用10×20的灰、白兩色的廣場磚鋪設圖案,設計人員畫出的一些備選圖案如圖所示.
[觀察思考]
圖1灰磚有1塊,白磚有8塊;圖2灰磚有4塊,白磚有12塊;以此類推.
[規律總結]
(1)圖4灰磚有 塊,白磚有 塊;圖n灰磚有 塊時,白磚有 塊;
[問題解決]
(2)是否存在白磚數恰好比灰磚數少1的情形,請通過計算說明你的理由.發布:2025/5/22 14:30:2組卷:522引用:11難度:0.6 -
 2.我國宋朝時期的數學家楊輝,曾將大小完全相同的圓彈珠逐層堆積,形成“三角垛”.如圖,第1個圖有1顆彈珠;第2個圖有3顆彈珠;第3個圖有6顆彈珠;第4個圖有10顆彈珠;…;用an表示第n個圖的彈珠數,若…+1a1+1a2+1a3+=1an,則n的值是( )20231012
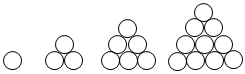
2.我國宋朝時期的數學家楊輝,曾將大小完全相同的圓彈珠逐層堆積,形成“三角垛”.如圖,第1個圖有1顆彈珠;第2個圖有3顆彈珠;第3個圖有6顆彈珠;第4個圖有10顆彈珠;…;用an表示第n個圖的彈珠數,若…+1a1+1a2+1a3+=1an,則n的值是( )20231012A.1012 B.2022 C.2023 D.2024 發布:2025/5/22 11:0:1組卷:214引用:4難度:0.6 -
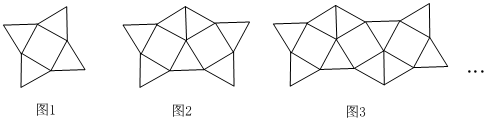
3.如圖是一組有規律的圖案,圖1是由1個正方形和4個正三角形組成的,共有5個基本圖形,圖2是由2個正方形和7個正三角形組成的,共有9個基本圖形,…依此規律,第n個圖案有 個基本圖形.(用含n的代數式表示)
 發布:2025/5/22 15:30:1組卷:181引用:2難度:0.7
發布:2025/5/22 15:30:1組卷:181引用:2難度:0.7


