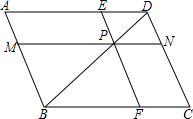
如圖，已知平行四邊形ABCD中，P是對角線BD上的一點，過P點作MN∥AD，EF∥CD，分別交AB、CD、AD、BC于M、N、E、F，設a=PM?PE，b=PN?PF．
（1）請判斷a與b的大小關系，并說明理由；
（2）當BPPD=2時，求S平行四邊形PEAMS△ABD的值．
BP
PD
=
2
S
平行四邊形
PEAM
S
△
ABD
【考點】相似三角形的判定與性質；平行四邊形的性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 10:30:2組卷：528引用：14難度：0.3
相似題
-
1．如圖，AE與BD相交于點C，AB=4，BC=2，AC=3，CD=6，CE=4．
（1）△ABC與△DEC是否相似？為什么？
（2）求DE的長．發布：2025/5/30 21:30:2組卷：39引用：2難度：0.5 -
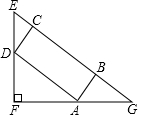2．如圖，在一個Rt△EFG的內部作一個矩形ABCD，其中點A和點D分別在兩直角邊上，BC在斜邊上，EF=30cm,FG=40cm,設AB=x cm.
（1）試用含x的代數式表示AD；
（2）設矩形ABCD的面積為s,當x為何值時，s的值最大，最大值是多少？發布：2025/5/30 22:0:2組卷：1257引用：5難度：0.5 -
3．如圖示，若△ABC內一點P滿足∠PAC=∠PBA=∠PCB，則點P為△ABC的布洛卡點．三角形的布洛卡點（Brocard point）是法國數學家和數學教育家克洛爾（A．L．Crelle 1780-1855）于1816年首次發現，但他的發現并未被當時的人們所注意，1875年，布洛卡點被一個數學愛好者法國軍官布洛卡（Brocard 1845-1922）重新發現，并用他的名字命名．問題：已知在等腰直角三角形DEF中，∠EDF=90°，若點Q為△DEF的布洛卡點，DQ=1，則EQ+FQ=（ ）發布：2025/5/30 22:0:2組卷：2024引用：14難度：0.7