某自行車廠為共享單車公司生產新樣式的單車，已知生產新樣式單車的固定成本為20000元，每生產一輛新樣式單車需要增加投入100元．根據初步測算，自行車廠的總收益（單位：元）滿足分段函數y=400x-12x2， 0＜x≤400 80000， x＞400
，其中x是新樣式單車的月產量（單位：輛），利潤=總收益-總成本．
（1）試將利潤用z元表示為月產量x的函數；
（2）當月產量x為多少件時利潤最大？最大利潤是多少？
400 x - 1 2 x 2 ， | 0 ＜ x ≤ 400 |
80000 ， | x ＞ 400 |
【考點】一次函數的應用；一元一次不等式的應用．
【答案】（1）z=
，（2）當月產量x為300件時利潤最大，最大利潤是25000元．
- 1 2 x 2 + 300 x - 20000 （ 0 ＜ x ≤ 400 ） |
60000 - 100 x （ x ＞ 400 ） |
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：203引用：2難度：0.5
相似題
-
1．小剛和小強在一條由西向東的公路上行走，出發時間相同，小強從A出發，小剛從A往東100米的B處出發，兩人到達C地后都停止．設兩人行走x分鐘后，小強、小剛離B的距離分別為y1、y2（m），y1、y2與x的函數關系如圖所示：
（1）根據圖象可得：A、C兩地間的距離為m；
（2）求a的值；
（3）求圖中點P的坐標，并解釋該點坐標所表示的實際意義．發布：2025/5/28 0:30:1組卷：96引用：2難度：0.5 -
2．某儀器廠計劃制造A、B兩種型號的儀器共80套，該公司所籌資金不少于2090萬元，但不超過2096萬元，且所籌資金全部用于制造儀器，兩種型號的制造成本和售價如下表：
（1）該廠對這兩種型號儀器有哪幾種制造方案？A B 成本（萬元/套） 25 28 售價（萬元/套） 30 34
（2）該廠應該選用哪種方案制造可獲得利潤最大？
（3）根據市場調查，每套B型儀器的售價不會改變，每套A型儀器的售價將會提高a萬元（a＞0），且所制造的兩種儀器可全部售出，問該廠又將如何制造才能獲得最大利潤？發布：2025/5/27 22:0:2組卷：176引用：4難度：0.5 -
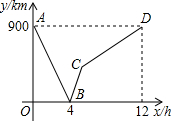3．一列快車從甲地駛往乙地，一列慢車從乙地駛往甲地，兩車同時出發，設慢車行駛的時間為x（h），兩車之間的距離為y（km），圖中的折線表示y與x之間的函數關系．根據圖象進行以下探究：
信息讀取：
（1）甲、乙兩地之間的距離為 km；
（2）請解釋圖中點B的實際意義；
圖象理解：
（3）求慢車和快車的速度；
（4）求線段BC所表示的y與x之間的函數關系式，并寫出自變量x的取值范圍；
問題解決：
（5）若第二列快車也從甲地出發駛往乙地，速度與第一列快車相同．在第一列快車與慢車相遇30分鐘后，第二列快車與慢車相遇．求第二列快車比第一列快車晚出發多少小時？發布：2025/5/27 22:30:1組卷：3645引用：56難度：0.5