閱讀材料，完成相應(yīng)任務(wù)：“賈憲三角”又稱(chēng)“楊輝三角”，在歐洲則稱(chēng)為“帕斯卡三角”（如圖所示），它揭示了（a+b）n（n為非負(fù)數(shù)）展開(kāi)式的各項(xiàng)系數(shù)的規(guī)律．
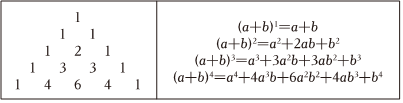
根據(jù)上述規(guī)律，完成下列問(wèn)題：
（1）直接寫(xiě)出（a+b）5=_____．
（2）（a+1）8的展開(kāi)式中a項(xiàng)的系數(shù)是_____．
（3）利用上述規(guī)律求115的值，寫(xiě)出過(guò)程．
【考點(diǎn)】二項(xiàng)式定理的應(yīng)用．
【答案】（1）a5+5a4b+10a3b2+10a2b3+5ab4+b5；
（2）8；
（3）161051．
（2）8；
（3）161051．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/10/27 17:0:2組卷：22引用：1難度：0.8
相似題
-
1．楊輝是我國(guó)古代數(shù)學(xué)史上一位著述豐富的數(shù)學(xué)家，著有《詳解九章算法》、《日用算法》和《楊輝算法》．楊輝三角的發(fā)現(xiàn)要比歐洲早500年左右，由此可見(jiàn)我國(guó)古代數(shù)學(xué)的成就是非常值得中華民族自豪的．楊輝三角本身包含了很多有趣的性質(zhì)，利用這些性質(zhì)，可以解決很多數(shù)學(xué)問(wèn)題，如開(kāi)方、數(shù)列等．
我們借助楊輝三角可以得到以下兩個(gè)數(shù)列的和.1+1+1+…+1=n；1+2+3+…+C1n-1=C2n
若楊輝三角中第三斜行的數(shù)：1，3，6，10，15，…構(gòu)成數(shù)列{an}，則關(guān)于數(shù)列{an}敘述正確的是（ ）發(fā)布：2024/11/27 6:30:2組卷：135引用：3難度：0.7 -
2．楊輝是中國(guó)南宋末年的一位杰出的數(shù)學(xué)家、教育家．楊輝三角是楊輝的一項(xiàng)重要研究成果，它的許多性質(zhì)與組合數(shù)的性質(zhì)有關(guān)，楊輝三角中蘊(yùn)藏了許多規(guī)律，如圖是一個(gè)11階楊輝三角．
（1）第20行中從左到右的第4個(gè)數(shù)為 ；
（2）若第n行中從左到右第7個(gè)與第9個(gè)數(shù)的比為，則n的值為 ．79發(fā)布：2024/12/29 4:30:2組卷：35引用：3難度：0.8 -
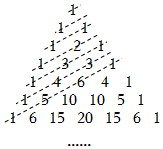3．“楊輝三角”是中國(guó)古代數(shù)學(xué)杰出的研究成果之一．如圖所示，由楊輝三角的左腰上的各數(shù)出發(fā)，引一組平行線，從上往下每條線上各數(shù)之和依次為1，1，2，3，5，8，13，……，則下列選項(xiàng)不正確的是（ ）發(fā)布：2024/12/29 12:0:2組卷：192引用：4難度：0.5