已知函數(shù)f（x）=cosx,
g
（
x
）
=
6
x
x
2
+
1
，若函數(shù)h（x）在
[
-
π
2
，
π
2
]
上的大致圖象如圖所示，則h（x）的解析式可能是（　　）

A．h（x）=f（x）+g（x）	B．h（x）=f（x）-g（x）
C． h （ x ） = f （ x ） g （ x ）	D．h（x）=f（x）g（x）

【答案】D

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/4/20 14:35:0組卷：59引用：3難度：0.7

相似題

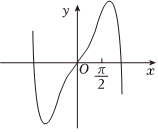1．已知函數(shù)f（x）的部分圖象如圖，則函數(shù)f（x）的解析式可能為（　　）
A．f（x）=（2^x+2^-x）sinx B．f（x）=（2^x-2^-x）sinx
C．f（x）=（2^x+2^-x）cosx D．f（x）=（2^x-2^-x）cosx
發(fā)布：2024/10/4 17:0:2組卷：79引用：2難度：0.7
解析
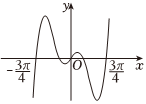2．已知函數(shù)f（x）的部分圖象如圖所示，則f（x）的解析式可能為（　　）
A．f（x）=（3^x+3^-x）sin2x B．f（x）=（3^x+3^-x）cos2x
C．f（x）=（3^x-3^-x）sin2x D．f（x）=（3^x-3^-x）cos2x
發(fā)布：2024/10/20 12:0:2組卷：238引用：5難度：0.5
解析
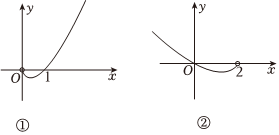3．函數(shù)y=f（x）的圖象如圖①所示，則如圖②所示的函數(shù)圖象所對應(yīng)的函數(shù)解析式可能為（　　）
A．
y
=
f
（
1
-
1
2
x
）
B．
y
=
-
f
（
1
-
1
2
x
）
C．y=f（4-2x） D．y=-f（4-2x）
發(fā)布：2024/10/17 8:0:2組卷：79引用：6難度：0.6
解析

相關(guān)試卷

A．f（x）=（2^x+2^-x）sinx	B．f（x）=（2^x-2^-x）sinx
C．f（x）=（2^x+2^-x）cosx	D．f（x）=（2^x-2^-x）cosx

A．f（x）=（3^x+3^-x）sin2x	B．f（x）=（3^x+3^-x）cos2x
C．f（x）=（3^x-3^-x）sin2x	D．f（x）=（3^x-3^-x）cos2x

A． y = f （ 1 - 1 2 x ）	B． y = - f （ 1 - 1 2 x ）
C．y=f（4-2x）	D．y=-f（4-2x）

已知函數(shù)f（x）=cosx,g（x）=6xx2+1，若函數(shù)h（x）在[-π2，π2]上的大致圖象如圖所示，則h（x）的解析式可能是（ ）