在正方形ABCD中，E、F分別為AD邊上的兩點(diǎn)，連接BF、CE并延長交于點(diǎn)Q，連接DQ，H為CQ上一點(diǎn)，連接BH、DH．
（1）如圖1，若H為CE的中點(diǎn)，且4DE=AB，DH=17，求線段BC的長；
（2）如圖2，過點(diǎn)H作HP∥BC，且HB=HP，連接BP，剛好交CH的中點(diǎn)G，當(dāng)∠QFE+∠QBH=90°時(shí)，求證：BP+2DQ=2CQ；
（3）如圖3，在（1）的條件下，點(diǎn)M為線段AD上一動點(diǎn)，連接CM，作BN⊥CM于點(diǎn)N，將△BCN沿BC翻折得到△BCN′，點(diǎn)S、R分別為線段BC、CN′上兩點(diǎn)，且BC=4CS，N′C=3N′R，連接BR、N′S交于點(diǎn)O，連接CO，請直接寫出△BCO面積的最大值．
17
2
【考點(diǎn)】四邊形綜合題．
【答案】（1）8；
（2）證明過程詳見解答；
（3）．
（2）證明過程詳見解答；
（3）
48
5
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/1 8:0:9組卷：258引用：1難度：0.5
相似題
-
1．如圖，四邊形ABCD中，AD∥BC，∠A=90°，AD=1厘米，AB=3厘米，BC=5厘米，動點(diǎn)P從點(diǎn)B出發(fā)以1厘米/秒的速度沿BC方向運(yùn)動，動點(diǎn)Q從點(diǎn)C出發(fā)以2厘米/秒的速度沿CD方向運(yùn)動，P，Q兩點(diǎn)同時(shí)出發(fā)，當(dāng)點(diǎn)Q到達(dá)點(diǎn)D時(shí)停止運(yùn)動，點(diǎn)P也隨之停止，設(shè)運(yùn)動時(shí)間為t秒（t＞0）．
（1）求線段CD的長；
（2）t為何值時(shí)，線段PQ將四邊形ABCD的面積分為1：2兩部分？
（3）伴隨P，Q兩點(diǎn)的運(yùn)動，線段PQ的垂直平分線為l.
①t為何值時(shí)，l經(jīng)過點(diǎn)C？
②求當(dāng)l經(jīng)過點(diǎn)D時(shí)t的值，并求出此時(shí)刻線段PQ的長．發(fā)布：2025/6/23 14:30:1組卷：1313引用：2難度：0.5 -
2．平行四邊形ABCD中，AB⊥AC，點(diǎn)E在邊AD上，連BE．
（1）如圖1，AC交BE于點(diǎn)G，若BE平分∠ABC，且∠DAC=30°，CG=2，請求出四邊形EGCD的面積；
（2）如圖2，點(diǎn)F在對角線AC上，且AF=AB，連BF，過點(diǎn)F作FH⊥BE于H，連AH并延長交CD于點(diǎn)M，點(diǎn)N在邊AD上，連MN．若AN=BF，2∠NMD=∠DAC+∠HBF，求證：HF+AH=AC．2
（3）如圖3，線段PO在線段BE上運(yùn)動，點(diǎn)R在邊BC上，連接CQ、PR．若BE平分∠ABC，∠DAC=30°，AB=，PQ=3，BC=4BR．請直接寫出線段CQ+PQ+PR的和的最小值以及此時(shí)△CQE的面積．32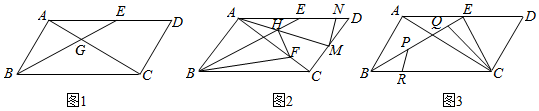
發(fā)布：2025/6/22 1:0:1組卷：261引用：3難度：0.5 -
3．如圖1，在正方形ABCD的外側(cè)，作兩個(gè)等邊三角形ADE和DCF，連接AF，BE．
（1）請判斷：AF與BE的數(shù)量關(guān)系是，位置關(guān)系是；
（2）如圖2，若將條件“兩個(gè)等邊三角形ADE和DCF”變?yōu)椤皟蓚€(gè)等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）問中的結(jié)論是否仍然成立？請作出判斷并給予說明；
（3）若三角形ADE和DCF為一般三角形，且AE=DF，ED=FC，第（1）問中的結(jié)論都能成立嗎？請直接寫出你的判斷．
發(fā)布：2025/6/23 16:0:1組卷：3585引用：23難度：0.5