如圖，已知AB為半圓O的直徑，P為半圓上的一個動點（不含端點），以OP、OB為一組鄰邊作?POBQ，連接OQ、AP，設OQ、AP的中點分別為M、N，連接PM、ON．
（1）試判斷四邊形OMPN的形狀，并說明理由．
（2）若點P從點B出發，以每秒15°的速度，繞點O在半圓上逆時針方向運動，設運動時間為ts.
①試求：當t為何值時，四邊形OMPN的面積取得最大值？并判斷此時直線PQ與半圓O的位置關系（需說明理由）；
②是否存在這樣的t,使得點Q落在半圓O內？若存在，請直接寫出t的取值范圍；若不存在，請說明理由．
【考點】圓的綜合題．
【答案】（1）四邊形OMPN為矩形，理由見解析過程；
（2）①當t=6s時，四邊形OMPN的面積取得最大值，PQ與半圓O相切；
（3）當8＜t＜12時，點Q落在半圓O內．
（2）①當t=6s時，四邊形OMPN的面積取得最大值，PQ與半圓O相切；
（3）當8＜t＜12時，點Q落在半圓O內．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：627引用：4難度：0.2
相似題
-
1．在矩形ABCD中，AB=6cm,BC=12cm,點P從點A出發，沿AB邊向點B以每秒1cm的速度移動，同時點Q從點B出發沿BC邊向點C以每秒2cm的速度移動P、Q兩點在分別到達B、C兩點后就停止移動，設兩點移動的時間為t秒，回答下列問題：
（1）如圖1，當t為幾秒時，△PBQ的面積等于5cm2？
（2）如圖2，當t=秒時，試判斷△DPQ的形狀，并說明理由；32
（3）如圖3，以Q為圓心，PQ為半徑作⊙Q．
①在運動過程中，是否存在這樣的t值，使⊙Q正好與四邊形DPQC的一邊（或邊所在的直線）相切？若存在，求出t值；若不存在，請說明理由；
②若⊙Q與四邊形DPQC有三個公共點，請直接寫出t的取值范圍．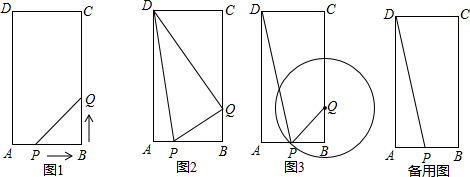
發布：2025/6/22 20:0:1組卷：554引用：8難度：0.3 -
2．如圖，已知直線與兩坐標軸分別交于A、B兩點，⊙C的圓心坐標為（-2，0），半徑為2，若D是⊙C上的一個動點，線段DA與y軸交于點E，則△ABE面積S的取值范圍是y=-3x+23．發布：2025/6/22 19:30:1組卷：340引用：3難度：0.7 -
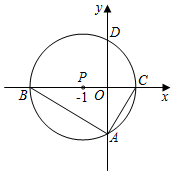3．如圖，以點P（-1，0）為圓心的圓，交x軸于B、C兩點（B在C的左側），交y軸于A、D兩點（A在D的下方），AD=2，將△ABC繞點P旋轉180°，得到△MCB．3
（1）求B、C兩點的坐標；
（2）請在圖中畫出線段MB、MC，并判斷四邊形ACMB的形狀（不必證明），求出點M的坐標；
（3）動直線l從與BM重合的位置開始繞點B順時針旋轉，到與BC重合時停止，設直線l與CM交點為E，點Q為BE的中點，過點E作EG⊥BC于G，連接MQ、QG．請問在旋轉過程中∠MQG的大小是否變化？若不變，求出∠MQG的度數；若變化，請說明理由．發布：2025/6/23 2:0:1組卷：676引用：30難度：0.1