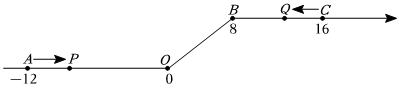
如圖，將一條數軸在原點O和點B處各折一下，得到一條“折線數軸”．圖中點A表示-12，點B表示8，點C表示16，我們稱點A和點C在數軸上相距28個長度單位．動點P從點A出發，以2單位/秒的速度沿著“折線數軸”的正方向運動，從點O運動到點B期間速度變為原來的一半，之后立刻恢復原速；同時，動點Q從點C出發，以1單位/秒的速度沿著數軸的負方向運動，從點B運動到點O期間速度變為原來的兩倍，之后也立刻恢復原速．設運動的時間為t秒．問：
（1）動點Q從點C運動至A點所需的時間是

24

24

秒；
（2）P、Q兩點相遇時，求出相遇的時間和點M所對應的數是多少；
（3）用含t代數式分別表示：點P在線段AO上運動時，所表示數是

-12+2t

-12+2t

；在線段OB上運動時，所表示數是

t-6

t-6

；在線段BC上運動時，所表示數是

8+2t

8+2t

；
（4）求當t為何值時，P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等．