在矩形ABCD中，AB=12，AD＞AB，P是邊AB上一點，把△PBC沿直線PC折疊，頂點B的對應點是點G，CG與AD交于點E，連接BE，∠BEC=90°，BE交PC于點F．
（1）當點E是AD的中點時，求證：△AEB≌△DEC；
（2）當AD=25，且AE＜DE時，求CFCP的值；
（3）當BE?EF=84時，求BP的值．
CF
CP
【考點】相似形綜合題．
【答案】（1）見解析過程；
（2）；
（3）7．
（2）
4
5
（3）7．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/5 8:0:7組卷：102引用：1難度：0.3
相似題
-
1．問題背景 如圖（1），已知△ABC∽△ADE，求證：△ABD∽△ACE；
嘗試應用 如圖（2），在△ABC和△ADE中，∠BAC=∠DAE=90°，∠ABC=∠ADE=30°，AC與DE相交于點F，點D在BC邊上，=ADBD，求3的值；DFCF
拓展創新 如圖（3），D是△ABC內一點，∠BAD=∠CBD=30°，∠BDC=90°，AB=4，AC=2，直接寫出AD的長．3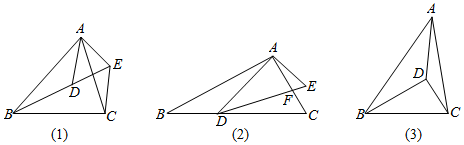
發布：2025/5/23 7:0:1組卷：11448引用：43難度：0.7 -
2．如圖1，在正方形ABCD中，點E、F分別在BC、CD上，且BE=DF，AE、AF分別與BD交于點G、H，過點G作GN⊥AF，垂足為M，交AD于點N．
（1）求證：AH=GN；
（2）若∠EAF=45°，求證：；AHAF=BGCF
（3）如圖2，過點G作GQ⊥AD，垂足為Q，交AF于點P．若GM=4MN，求的值．APGP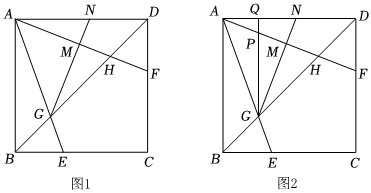
發布：2025/5/23 7:0:1組卷：331引用：2難度：0.1 -
3．【初步嘗試】
（1）如圖1，在正方形ABCD中，點E，F分別為AB、AD邊上的點且DE⊥CF，求證：DE=CF．
（2）【思考探究】
如圖2，在矩形ABCD中，AB=3，BC=2，點E為BC中點，點F為AE上一點，連接CF、DF且CF=CD，求DF的值．
（3）【拓展應用】
如圖3，在四邊形ABCD中，∠DAB=90°，∠ABC=45°，，點E、F分別在線段AB、AD上，且CE⊥BF．直接寫出BC=23AB的值．CEBF
發布：2025/5/23 7:0:1組卷：409引用：1難度：0.1