古希臘畢達哥拉斯學派的“三角形數”是一列點（或圓球）在等距的排列下可以形成正三角形的數，如1，3，6，10，15，…．我國宋元時期數學家朱世杰在《四元玉鑒》中所記載的“垛積術”其中的“落一形”堆垛就是每層為“三角形數”的三角錐的錐垛（如圖所示頂上一層1個球，下一層3個球，再下一層6個球），若一個“落一形”三角錐垛有10層，則該堆垛球的總個數為（　　）

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/30 3:0:1組卷：87引用：2難度：0.6

相似題

1．如圖，Rt△ABC中，∠ACB=90°，CA=CB，∠BAD=∠ADE=60°，DE=3，AB=10，CE平分∠ACB，DE與CE相交于點E，則AD的長為（　　）
A．4 B．13 C．6.5 D．7
發布：2025/5/31 8:0:1組卷：752引用：8難度：0.5
解析
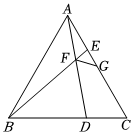2．如圖，等邊三角形ABC的邊長為
2
3
，點D、E分別是邊BC、AC的動點，且AE=CD，連接AD、BE交于點F，G為AC的中點，連接FG，則線段FG長的最小值為
．
發布：2025/5/31 8:30:1組卷：502引用：2難度：0.4
解析
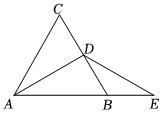3．如圖，△ABC是等邊三角形，D點是BC的中點，延長AB到E，使BE=BD，若∠BED=30°，則∠ADE=
度．
發布：2025/5/31 10:0:1組卷：370引用：3難度：0.7
解析

相關試卷

1．如圖，Rt△ABC中，∠ACB=90°，CA=CB，∠BAD=∠ADE=60°，DE=3，AB=10，CE平分∠ACB，DE與CE相交于點E，則AD的長為（ ）