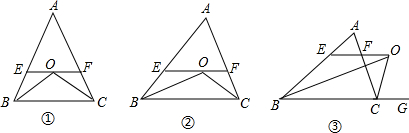
（1）如圖①，△ABC中，AB=AC，∠ABC、∠ACB的平分線交于O點，過O點作EF∥BC交AB、AC于E、F．圖中有 55個等腰三角形．猜想：EF與BE、CF之間有怎樣的關(guān)系，并說明理由．
（2）如圖②，若AB≠AC，其他條件不變，圖中有 22個等腰三角形．
它們是 △BEO，△CFO△BEO，△CFO．EF與BE、CF間的關(guān)系是 EF=BE+CFEF=BE+CF．
（3）如圖③，若△ABC中∠ABC的平分線與三角形外角平分線交于O，過O點作OE∥BC交AB于E，交AC于F．這時圖中有 22個等腰三角形．EF與BE、CF關(guān)系又如何？說明你的理由．
【考點】三角形綜合題．
【答案】5；2；△BEO，△CFO；EF=BE+CF；2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/19 2:0:1組卷：139引用：4難度：0.3
相似題
-
1．在△ABC和△EDC中，∠ACB=∠ECD=90°，BC=k?AC，CD=k?CE．
（1）如圖1，當(dāng)k=1時，探索AE與BD的關(guān)系；
（2）如圖2，當(dāng)k≠1時，請?zhí)剿鰽E與BD的關(guān)系，并證明；
（3）如圖3，在（2）的條件下，分別在BD、AE上取點M、N，使得BD=m?MD，AE=m?NE，試探索CN與CM的關(guān)系，并證明．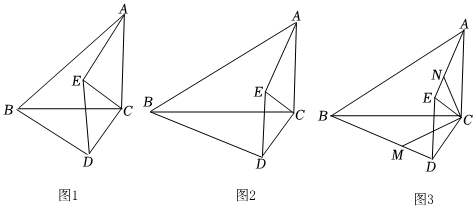
發(fā)布：2025/5/22 16:30:1組卷：88引用：1難度：0.1 -
2．在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，連接CE．
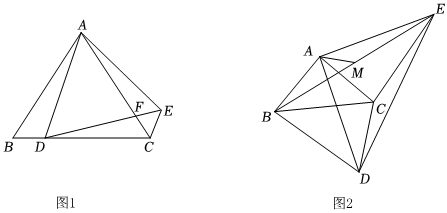
（1）如圖1，若點D在BC邊上，AC，DE相交于F點．
①求證：BD=CE；
②若AF=DF，AB=5，BC=6，求BD的長．
（2）如圖2，若∠BAC=90°，M為BE的中點，連接AM，求證：AM⊥CD．發(fā)布：2025/5/22 16:30:1組卷：211引用：3難度：0.1 -
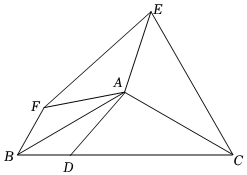3．如圖，已知△ABC，AB=AC，BC=6，∠BAC=120°，點D在BC上（不與B、C重合），連接AD，分別將△ABD和△ACD沿直線AB、AC翻折得到△ABF和△ACE，連接EF，給出下列結(jié)論：
①EF=AF；3
②當(dāng)AD⊥AF時，CD的長為2；3
③當(dāng)D、A、F三點共線時，四邊形ADCE是菱形；
④△AEF面積的最小值為．334
則正確結(jié)論有 ．（填序號）發(fā)布：2025/5/22 18:30:2組卷：430引用：2難度：0.2