如圖，CD∥EF，AC⊥AE，且∠α和∠β的度數滿足方程組2∠α+∠β=235° ∠β-∠α=70°
（1）求∠α和∠β的度數．
（2）求證：AB∥CD．
（3）求∠C的度數．
2 ∠ α + ∠ β = 235 ° |
∠ β - ∠ α = 70 ° |
【考點】平行線的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：684引用：5難度：0.5
相似題
-
1．如圖，AD∥BC，∠1=∠B．
（1）AB與DE平行嗎？請說明理由；
（2）若∠A=120°，CD⊥AD，求∠EDC的度數．
請在下面的解答過程的空格內填空或在橫線上填寫理由．
解：（1）AB∥DE，理由如下：
∵AD∥BC，（已知）
∴∠1=∠.
又∵∠1=∠B，（已知）
∴∠B=∠.
∴∥．
（2）∵AD∥BC，（已知）
∴∠A+∠=180°，
∴∠B=180°-∠A=°．（等式的性質）
又∵∠1=∠B，（已知）
∴∠1=°．（等量代換）
∵CD⊥AD，（已知）
∴∠ADC=°．（垂直的定義）
∴∠EDC=∠-∠=°-°=°．發布：2025/5/31 14:0:2組卷：670引用：1難度：0.3 -
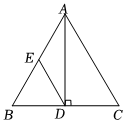2．如圖，已知AB=AC，AD⊥BC于D，DE=AE．
（1）求證：DE∥AC；
（2）若∠C=60°，AC=6，求AD的長．發布：2025/5/31 12:30:1組卷：251引用：3難度：0.7 -
3．閱讀下列推理過程，在括號中填寫理由．
如圖，已知AD⊥BC，EF⊥BC，∠1=∠2．試證明：DG∥BA．
解：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB=∠ADB=90°（ ）．
∴∥（ ）．
∴∠1=∠BAD（ ）．
又∵∠1=∠2（已知），
∴（ ）．
∴DG∥BA（ ）發布：2025/5/31 15:0:2組卷：810引用：8難度：0.7