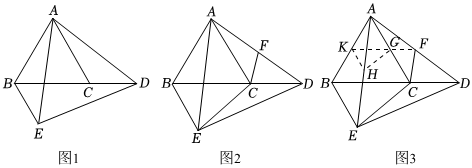
探究式學習是新課程倡導的重要學習方式，某興趣小組擬做以下探究．等邊△ABC的BC邊延長線上有一動點D，連接AD，以AD為邊作等邊△ADE，連接BE．
【初步感知】
（1）如圖1，當D點不與C點重合時，興趣小組探究得出結論：
①BE=CD；
②∠DBE的度數是定值，請你寫出他們的證明過程；
【深入探究】
（2）如圖2，點F是線段AD的中點，連接CF，猜想CF和CE的數量關系．
小明猜想：假設D點剛好和C點重合時，猜想出結論是：CF=12CECF=12CE；
小紅也提出了自己的想法：因為題設中提到了中點，所以想到添加中點構造輔助線進行轉化．如圖3，是小紅添加的輔助線，點G，點H，點K分別是線段AC，AE，AB的中點，請你幫她繼續完成證明過程．
【拓展運用】
（3）在（2）的條件下，若等邊△ABC的邊長是3，則點D從點C向右運動過程中，CF的最小值是 334334．（直接寫出答案，無需證明）
CF
=
1
2
CE
CF
=
1
2
CE
3
3
4
3
3
4
【考點】三角形綜合題．
【答案】；
CF
=
1
2
CE
3
3
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/23 4:0:8組卷：53引用：2難度：0.2
相似題
-
1．【問題探究】在學習三角形中線時，我們遇到過這樣的問題：如圖①，在△ABC中，點D為BC邊上的中點，AB=4，AC=6，求線段AD長的取值范圍．我們采用的方法是延長線段AD到點E，使得AD=DE，連結CE，可證△ABD≌△ECD，可得CE=AB=4，根據三角形三邊關系可求AD的范圍，我們將這樣的方法稱為“三角形倍長中線”．則AD的范圍是：．
【拓展應用】
（1）如圖②，在△ABC中，BC=2BD，AD=3，AC=2，∠BAD=90°，求AB的長．10
（2）如圖③，在△ABC中，D為BC邊的中點，分別以AB、AC為直角邊向外作直角三角形，且滿足∠ABE=∠ACF=30°，連結EF，若AD=2，則EF=．（直接寫出）3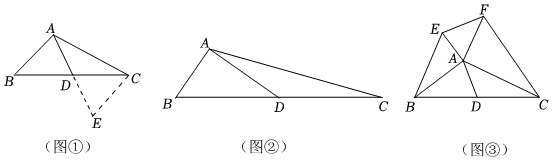
發布：2025/5/26 8:0:5組卷：411引用：5難度：0.4 -
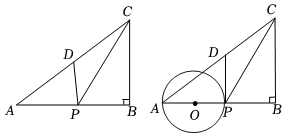2．如圖①，在△ABC中，∠ABC=90°，AC=10，BC=6，D點為AC邊的中點．點P在邊AB上運動（點P不與A、B重合），連結PD、PC．設線段AP的長度為x.
（1）求AB的長．
（2）當△APD是等腰三角形時，求這個等腰三角形的腰長．
（3）連結PD、PC，當PD+PC取最小值時，求x的值．
（4）如圖②，取AP的中點為O，以點O為圓心，以線段AP的長為直徑的圓與線段PD有且只有一個公共點時，直接寫出x的取值范圍．發布：2025/5/26 6:30:2組卷：176引用：1難度：0.3 -
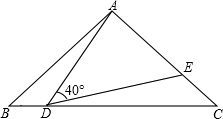3．如圖，在△ABC中，AB=AC=2，∠B=40°，點D在線段BC上運動（D不與B、C重合），連接AD，作∠ADE=40°，DE交線段AC于E．
（1）當∠BDA=115°時，∠BAD=°，∠DEC=°；
（2）當DC等于多少時，△ABD與△DCE全等？請說明理由；
（3）在點D的運動過程中，△ADE的形狀可以是等腰三角形嗎？若可以，請直接寫出∠BDA的度數．若不可以，請說明理由．發布：2025/5/26 2:30:2組卷：976引用：8難度：0.3