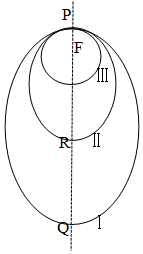
 如圖所示,“嫦娥一號”探月衛星沿地月轉移軌道飛向月球,在月球附近一點P變軌進入以月球球心F為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛星在P點第二次變軌進入仍以F為一個焦點的橢圓軌道Ⅱ繞月飛行,最終衛星在P點第三次變軌進入以F為圓心的圓形軌道Ⅲ繞月飛行.若用2c1和2c2分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用2a1和2a2分別表示橢圓軌道Ⅰ和Ⅱ的長軸的長,給出下列式子:
如圖所示,“嫦娥一號”探月衛星沿地月轉移軌道飛向月球,在月球附近一點P變軌進入以月球球心F為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛星在P點第二次變軌進入仍以F為一個焦點的橢圓軌道Ⅱ繞月飛行,最終衛星在P點第三次變軌進入以F為圓心的圓形軌道Ⅲ繞月飛行.若用2c1和2c2分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用2a1和2a2分別表示橢圓軌道Ⅰ和Ⅱ的長軸的長,給出下列式子:
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a1<c2a2;④c1a1>c2a2;其中正確式子的序號是( )
c
1
a
1
<
c
2
a
2
c
1
a
1
>
c
2
a
2
【考點】橢圓的離心率與橢圓形狀的關系.
【答案】D
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:69引用:2難度:0.7
相似題
-
1.已知P為橢圓
外一點,F1(-c,0),F2(c,0)分別為橢圓C的左、右焦點,|PF2|=x2a2+y2b2=1(a>b>0),線段PF1,PF2分別交橢圓于|F1F2|,PF1?PF2=6c2,設橢圓離心率為e,則下列說法正確的有( )M,N,F1M=λF1P,F2N=μF2PA.若e越大,則λ越大 B.若M為線段PF1的中點,則 e=3-1C.若 ,則μ=13e=13-14D. λμ=2+e33-4e發布:2024/8/1 8:0:9組卷:16引用:1難度:0.5 -
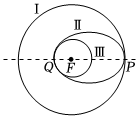 2.如圖所示,“嫦娥五號”月球探測器飛行到月球附近時,首先在以月球球心F為圓心的圓形軌道Ⅰ上繞月球飛行,然后在P點處變軌進入以F為一個焦點的橢圓軌道Ⅱ繞月球飛行,最后在Q點處變軌進入以F為圓心的圓形軌道Ⅲ繞月球飛行,設圓形軌道Ⅰ的半徑為R,圓形軌道Ⅲ的半徑為r,則( )
2.如圖所示,“嫦娥五號”月球探測器飛行到月球附近時,首先在以月球球心F為圓心的圓形軌道Ⅰ上繞月球飛行,然后在P點處變軌進入以F為一個焦點的橢圓軌道Ⅱ繞月球飛行,最后在Q點處變軌進入以F為圓心的圓形軌道Ⅲ繞月球飛行,設圓形軌道Ⅰ的半徑為R,圓形軌道Ⅲ的半徑為r,則( )A.軌道Ⅱ的長軸長為R+r B.軌道Ⅱ的焦距為R-r C.若R不變,r越小,軌道Ⅱ的短軸長越大 D.若r不變,R越大,軌道Ⅱ的離心率越小 發布:2024/8/7 8:0:9組卷:108引用:2難度:0.5 -
3.已知焦點在x軸上的橢圓方程為
+x24a=1,隨著a的增大該橢圓的形狀( )y2a2-1A.越接近于圓 B.越扁 C.先接近于圓后越扁 D.先越扁后接近于圓 發布:2024/10/2 17:0:2組卷:559引用:10難度:0.7


