2021-2022學年浙江省杭州二中濱江校區高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知向量

  a

  =（-2，3，-1），

  b

  =（4，m,n），且

  a

  =t

  b

  ，其中m,n∈R，則m+n=（　　）

  A．4

  B．-4

  C．2

  D．-2
  組卷：9引用：1難度：0.9

  解析

• 2．若圓x²+y²-6x+6y+14=0關于直線l：ax+4y-6=0對稱，則實數a的值（　　）

  A．2

  B．3

  C．5

  D．6
  組卷：15引用：1難度：0.7

  解析

• 3．已知過原點的平面α的一個法向量是

  m

  =

  （

  -

  2

  ，-

  1

  ，

  2

  ）

  ，點P（2，2，0）是平面α外的一點，則點P到平面α的距離是（　　）

  A．1

  B． 3 2 2

  C．2

  D． 2 2
  組卷：9引用：1難度：0.7

  解析

• 4．原點到直線l：3x+4y-2+λ（2x+y+2）=0的距離的最大值為（　　）

  A． 2 5

  B． 2 2

  C． 2 2 5

  D． 4 2 5
  組卷：521引用：4難度：0.8

  解析

• 5．過點A（-5，-1）的直線l與圓（x+3）²+（y-5）²=4相切，則直線l的方程為（　　）

  A．y=-1或4x+3y+23=0	B．y=-1或4x-3y+17=0
  C．x=-5或4x+3y+23=0	D．x=-5或4x-3y+17=0
  組卷：375引用：5難度：0.7

  解析

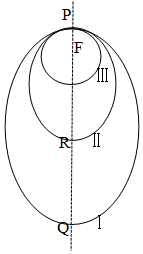• 6．如圖所示，“嫦娥一號”探月衛星沿地月轉移軌道飛向月球，在月球附近一點P變軌進入以月球球心F為一個焦點的橢圓軌道Ⅰ繞月飛行，之后衛星在P點第二次變軌進入仍以F為一個焦點的橢圓軌道Ⅱ繞月飛行，最終衛星在P點第三次變軌進入以F為圓心的圓形軌道Ⅲ繞月飛行．若用2c₁和2c₂分別表示橢圓軌道Ⅰ和Ⅱ的焦距，用2a₁和2a₂分別表示橢圓軌道Ⅰ和Ⅱ的長軸的長，給出下列式子：
  ①a₁+c₁=a₂+c₂；②a₁-c₁=a₂-c₂；③

  c

  1

  a

  1

  ＜

  c

  2

  a

  2

  ；④

  c

  1

  a

  1

  ＞

  c

  2

  a

  2

  ；其中正確式子的序號是（　　）

  A．①③

  B．②③

  C．①④

  D．②④
  組卷：69引用：2難度：0.7

  解析

• 7．已知集合

  M

  =

  {

  （

  x

  ,

  y

  ）

  |

  2 x - y + 1 ≥ 0

  x + y - 1 ≤ 0

  x - 2 y - 1 ≤ 0

  ，集合N={（x,y）|xcosθ+ysinθ≥r,r≥0}，若M∩N≠?，則（　　）

  A．0＜r≤1

  B． 1 ≤ r ≤ 2

  C． r ≥ 2

  D． 0 ≤ r ≤ 2
  組卷：3引用：1難度：0.4

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．在①AE=2，②AC⊥BD，③∠EAB=∠EBA，這三個條件中選擇一個，補充在下面問題中，并解答．
  如圖，在五面體ABCDE中，已知____，AC⊥BC，ED∥AC，且AC=BC=2ED=2，DC=DB=

  3

  ．
  （Ⅰ）求證：平面ABE⊥平面ABC；
  （Ⅱ）線段BC上是否存在一點F，使得平面AEF與平面ABE的夾角的余弦值等于

  5

  43

  43

  ？若存在，求

  BF

  BC

  的值；若不存在，說明理由．
  組卷：133引用：3難度：0.5

  解析

• 22．已知橢圓C：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  的左、右焦點分別為F₁、F₂，經過點F₁且傾斜角為θ

  （

  0

  ＜

  θ

  ＜

  π

  2

  ）

  的直線l與橢圓交于A、B兩點（其中點A在x軸上方）．將平面xOy沿x軸折疊，使y軸正半軸和x軸所確定的半平面（平面AF₁F₂）與y軸負半軸和x軸所確定的半平面（平面BF₁F₂）互相垂直．
  （1）若

  θ

  =

  π

  3

  ，求折疊后|AF₁|+|BF₁|-|AB|的值；
  （2）求折疊后的線段AB長度的取值范圍，并說明理由．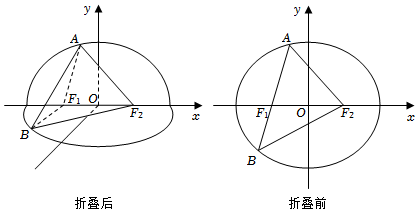
  
  組卷：176引用：3難度：0.2

  解析