綜合與實踐
問題情境
在學習了《勾股定理》和《實數》后,某班同學以“已知三角形三邊的長度,求三角形面積”為主題開展了數學活動.
操作發現
“畢達哥拉斯”小組的同學想到借助正方形網格解決問題.如圖1是6×6的正方形網格,每個小正方形的邊長均為1,每個小正方形的頂點稱為格點.在圖1中畫出△ABC,其頂點A,B,C都是格點,同時構造正方形BDEF,使它的頂點都在格點上,且它的邊DE,EF分別經過點C、A,他們借助此圖求出了△ABC的面積.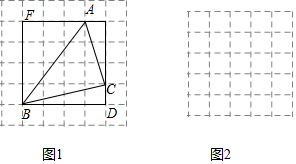
(1)在圖1中,所畫的△ABC的三邊長分別是AB=55,BC=1717,AC=1010;△ABC的面積為132132.
實踐探究
(2)在圖2所示的正方形網格中畫出△DEF(頂點都在格點上),使DE=5,DF=13,EF=20,并寫出△DEF的面積.
繼續探究
“秦九韶”小組的同學想到借助曾經閱讀的數學資料:
已知三角形的三邊長分別為a、b、c,求其面積,對此問題中外數學家曾經進行過深入研究.古希臘的幾何學家海倫(Heron,約公元50年),在他的著作《度量》一書中,給出了求其面積的海倫公式S=p(p-a)(p-b)(p-c)其中p=a+b+c2①
我國南宋時期數學家秦九韶(約1202~1261),給出了著名的秦九韶公式
S=14[a2b2-(a2+b2-c22)2].②
(3)一個三角形的三邊長依次為5,6,7,請你從上述材料中選用適當的公式求這個三角形的面積.(寫出計算過程)
17
17
10
10
13
2
13
2
5
13
20
S
=
p
(
p
-
a
)
(
p
-
b
)
(
p
-
c
)
其中
p
=
a
+
b
+
c
2
①
S
=
1
4
[
a
2
b
2
-
(
a
2
+
b
2
-
c
2
2
)
2
]
.
②
5
6
7
【答案】5;;;
17
10
13
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/5 9:0:8組卷:496引用:4難度:0.7
相似題
-
 1.如圖,AB為⊙O的直徑,弦CD⊥AB于點E,若AE=8,BE=2,則AC的長度為( )
1.如圖,AB為⊙O的直徑,弦CD⊥AB于點E,若AE=8,BE=2,則AC的長度為( )A.5 B.4 C.4 5D.8 發布:2025/5/24 21:30:1組卷:157引用:4難度:0.6 -
 2.在正方形網格中,每個小正方形的頂點稱為格點.如圖,點A,B,C,D均在格點上,連接AC,BD相交于點E,若小正方形的邊長為1,則點E到AB的距離為 .發布:2025/5/24 21:30:1組卷:214引用:1難度:0.7
2.在正方形網格中,每個小正方形的頂點稱為格點.如圖,點A,B,C,D均在格點上,連接AC,BD相交于點E,若小正方形的邊長為1,則點E到AB的距離為 .發布:2025/5/24 21:30:1組卷:214引用:1難度:0.7 -
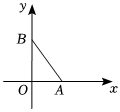 3.如圖,在平面直角坐標系中,點A、B的坐標分別為(3,0),(0,4),P為x軸上一動點,若△ABP是等腰三角形,則所有滿足條件的點P的坐標為 .發布:2025/5/24 22:30:1組卷:85引用:1難度:0.7
3.如圖,在平面直角坐標系中,點A、B的坐標分別為(3,0),(0,4),P為x軸上一動點,若△ABP是等腰三角形,則所有滿足條件的點P的坐標為 .發布:2025/5/24 22:30:1組卷:85引用:1難度:0.7


