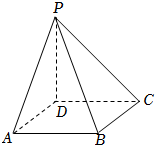
如圖，四棱錐P-ABCD的底面為正方形，PD⊥底面ABCD．設平面PAD與平面PBC的交線為l.
（1）證明：l⊥平面PDC；
（2）已知PD=AD=1，Q為l上的點且，DA=mPQ（m＞0），求PB與平面QCD所成角的正弦值的最大值．
DA
=
m
PQ
【考點】空間向量法求解直線與平面所成的角；直線與平面垂直．
【答案】（1）證明見解答；（2）．
6
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：204引用：4難度：0.4
