2022-2023學年湖南省長沙市雅禮中學高二（上）入學數學試卷

一、單選題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．已知復數z=1+i（i是虛數單位），則

  z

  2

  +

  2

  z

  -

  1

  =（　　）

  A．2+2i

  B．2-2i

  C．2i

  D．-2i
  組卷：156引用：3難度：0.8

  解析

• 2．已知集合A={x|x²-4≤0}，B={x|2x+a≤0}，若A∪B=B，則實數a的取值范圍是（　　）

  A．a＜-2

  B．a≤-2

  C．a＞-4

  D．a≤-4
  組卷：645引用：5難度：0.7

  解析

• 3．四棱錐P-ABCD的頂點都在球O的球面上，ABCD是邊長為3

  2

  的正方形，若四棱錐P-ABCD體積的最大值為54，則球O的表面積為（　　）

  A．36π

  B．64π

  C．100π

  D．144π
  組卷：144引用：5難度：0.6

  解析

• 4．如圖，在大小為45°的二面角A-EF-D中，四邊形ABFE與CDEF都是邊長為1的正方形，則B與D兩點間的距離是（　　）

  A． 3

  B． 2

  C．1

  D． 3 - 2
  組卷：677引用：13難度：0.7

  解析

• 5．將曲線C₁：

  y

  =

  2

  cos

  （

  2

  x

  -

  π

  6

  ）

  上的點向右平移

  π

  6

  個單位長度，再將各點橫坐標縮短為原來的

  1

  2

  ，縱坐標不變，得到曲線C₂，則C₂的方程為（　　）

  A．y=2sin4x	B． y = 2 sin （ 4 x - π 3 ）
  C．y=2sinx	D． y = 2 sin （ x - π 3 ）
  組卷：172引用：2難度：0.7

  解析

• 6．若定義在R的奇函數f（x）在（-∞，0）單調遞減，且f（2）=0，則滿足xf（x-1）≥0的x的取值范圍是（　　）

  A．[-1，1]∪[3，+∞）

  B．[-3，-1]∪[0，1]

  C．[-1，0]∪[1，+∞）

  D．[-1，0]∪[1，3]
  組卷：697引用：82難度：0.6

  解析

• 7．已知l,b表示不同的直線，α，β表示不同的平面，則下列說法正確的是（　　）

  A．若l⊥α，b⊥l,則b∥α

  B．若l,b?α，l∥β，b∥β，則α∥β

  C．若l∥α，b⊥β，l∥b,則α⊥β

  D．若α∩β=b,l?α，l⊥b,則α⊥β
  組卷：51引用：1難度：0.6

  解析

四、解答題（本大題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．）

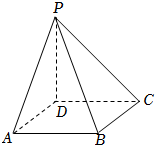• 21．如圖，四棱錐P-ABCD的底面為正方形，PD⊥底面ABCD．設平面PAD與平面PBC的交線為l.
  （1）證明：l⊥平面PDC；
  （2）已知PD=AD=1，Q為l上的點且，

  DA

  =

  m

  PQ

  （m＞0），求PB與平面QCD所成角的正弦值的最大值．
  組卷：204引用：4難度：0.4

  解析

• 22．已知二次函數f（x）=ax²+bx+1（a,b∈R，a＞0），設方程f（x）=x的兩個實數根為x₁和x₂．
  （1）如果x₁＜2＜x₂＜4，設二次函數f（x）的對稱軸為x=x₀，求證：x₀＞-1；
  （2）如果|x₁|＜2，|x₂-x₁|=2，求b的取值范圍．
  組卷：151引用：18難度：0.5

  解析