數(shù)學(xué)探究小組利用一些三角形彩紙裁剪面積最大的內(nèi)接正方形，他們就有關(guān)問(wèn)題進(jìn)行了探究：
定義：如果一個(gè)正方形的四個(gè)頂點(diǎn)都在一個(gè)三角形的邊上，那么我們就把這個(gè)正方形叫做三角形的內(nèi)接正方形．
作圖：如圖1，正方形DEFG的頂點(diǎn)E，F(xiàn)在邊AB上，頂點(diǎn)D在邊AC上，在△ABC及其內(nèi)部，以A為位似中心，作正方形DEFG的位似正方形D′E′F′G′，且使正方形D′E′F′G′的面積最大．
實(shí)踐操作：
（1）第一小組拿到的鈍角三角形原材料，你認(rèn)為在鈍角三角形中存在 11個(gè)內(nèi)接正方形；
（2）第二小組拿到的是直角三角形原材料，小明說(shuō)：在直角三角形中，兩個(gè)頂點(diǎn)都在斜邊上的內(nèi)接正方形的面積較大．小麗同學(xué)認(rèn)為他的結(jié)論不正確，她通過(guò)計(jì)算腰長(zhǎng)為1的等腰直角三角形（如圖2和圖3）的情況給予說(shuō)明，請(qǐng)你幫助小麗同學(xué)完成計(jì)算和說(shuō)理過(guò)程；
（3）第三小組拿到的是不等邊銳角三角形原材料，小華同學(xué)認(rèn)為：在不等邊銳角三角形中，兩個(gè)頂點(diǎn)都在較大邊上的內(nèi)接正方形的面積反而較小．小華同學(xué)已經(jīng)寫出了題設(shè)條件，請(qǐng)你幫助他完成推理過(guò)程．如圖4，設(shè)銳角△ABC的三條邊分別為a、b、c不妨設(shè)a＞b＞c,三條邊上的對(duì)應(yīng)高分別為ha、hb、hc，內(nèi)接正方形的邊長(zhǎng)分別為xa、xb、xc．
【考點(diǎn)】相似形綜合題．
【答案】1
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：338引用：2難度：0.1
相似題
-
1．在Rt△ABC中，∠BAC=90°，AB=AC，在Rt△ADE中，∠DAE=90°，2AD=AB，2AE=AC，連接DE，AN⊥BC，垂足為N，AM⊥DE，垂足為M．
（1）觀察猜想
圖①中，點(diǎn)D，E分別在AB，AC上時(shí)，的值為 ；BDCE的值為 ．BDMN
（2）探究證明
如圖②，將△ADE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)，旋轉(zhuǎn)角為α（0°＜α＜360°），連接BD，CE，判斷問(wèn)題（1）中的數(shù)量關(guān)系是否仍然存在，并證明；
（3）拓展延伸
在△ADE旋轉(zhuǎn)的過(guò)程中，設(shè)直線CE與BD相交于點(diǎn)F，若∠CAE=90°，AB=6，請(qǐng)直接寫出線段BF的長(zhǎng)．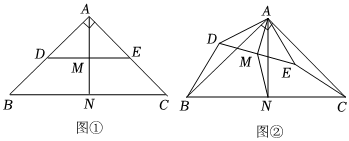
發(fā)布：2025/5/23 17:0:1組卷：518引用：1難度：0.1 -
2．【實(shí)踐操作】：
第一步：如圖①，將矩形紙片ABCD沿過(guò)點(diǎn)D的直線折疊，使點(diǎn)A落在CD上的A'處，得到折痕DE，然后把紙片展平．
第二步：如圖②，將圖中的矩形紙片ABCD沿過(guò)點(diǎn)E的直線折疊，點(diǎn)C恰好落在AD上的點(diǎn)C'處，點(diǎn)B落在B'處，得到折痕EF，B'C'交AB于點(diǎn)M，C'F交DE于點(diǎn)N，再把紙片展平．
【問(wèn)題解決】：
（1）如圖①，四邊形AEA'D的形狀是 ；
（2）如圖②，線段MC'與ME是否相等？若相等，請(qǐng)給出證明；若不相等，請(qǐng)說(shuō)明理由；
（3）如圖②，若AC'=3cm,DC'=6cm,則MC'=，=．DNEN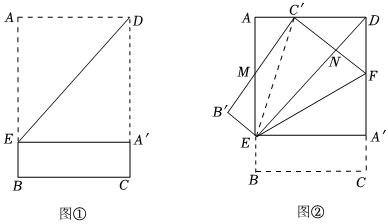
發(fā)布：2025/5/23 19:0:2組卷：311引用：3難度：0.1 -
3．問(wèn)題提出
（1）如圖①，在△ABC中，點(diǎn)D、E、F分別為邊AB、AC、BC的中點(diǎn)，DE∥BC，BC=8，AF交DE于點(diǎn)G，則DG的長(zhǎng)為 ；
問(wèn)題探究
（2）如圖②，在等腰直角△ABC中，∠C=90°，AC=4，點(diǎn)D為線段CB上一動(dòng)點(diǎn)（點(diǎn)D不與點(diǎn)B、C重合），以AD為腰且在AD的右側(cè)作等腰直角△ADF，∠ADF=90°，AB與FD交于點(diǎn)E，連接BF，求證：△ACD∽△ABF；
問(wèn)題解決
（3）如圖是郊外一空地，為了美化生態(tài)環(huán)境，現(xiàn)要將這塊地打造成一個(gè)公園，在空地一側(cè)挖一個(gè)四邊形的人工湖CDQP，點(diǎn)P、Q分別在邊AB、AD上，且滿足PB=AQ，已知AB=AD，∠ACB=∠BAD=90°，AB=500m,BC=300m,為了滿足湖周邊的建設(shè)用地需要，人工湖的面積需盡可能小，設(shè)PB的長(zhǎng)為x（m），四邊形CDQP的面積為S（m2）．
①求S與x之間的函數(shù)關(guān)系式；
②求人工湖面積的最小值及此時(shí)AQ的長(zhǎng)．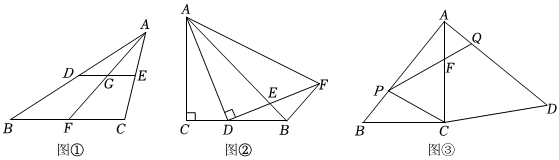
發(fā)布：2025/5/23 16:0:1組卷：259引用：1難度：0.3
相關(guān)試卷