如圖，拋物線C1與x軸交于A（-3，0），B（1，0）兩點，與y軸交于點C（0，3），點D為拋物線C1的頂點．
（1）求拋物線C1的表達(dá)式及點D坐標(biāo)；
（2）將拋物線C1關(guān)于點B對稱后的拋物線記為C2．點P是x軸上一點，請問在C2上是否存在一點Q，使以B，C，P，Q為頂點的四邊形是以BC為邊的平行四邊形？若存在，請求出點Q的坐標(biāo)；若不存在，請說明理由．
?
【考點】二次函數(shù)綜合題．
【答案】（1）y=-x2-2x+3，頂點D（-1，4）；
（2）點Q的坐標(biāo)為（3+，3）或（3-，3）或（4，-3）．
（2）點Q的坐標(biāo)為（3+
7
7
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/7 8:0:9組卷：536引用：1難度：0.3
相似題
-
1．如圖，拋物線y=
x2-2x-6與x軸相交于點A、點B，與y軸相交于點C．12
（1）請直接寫出點A，B，C的坐標(biāo)；
（2）若點P是拋物線BC段上的一點，當(dāng)△PBC的面積最大時求出點P的坐標(biāo)，并求出△PBC面積的最大值；
（3）點F是拋物線上的動點，作FE∥AC交x軸于點E，是否存在點F，使得以A、C、E、F為頂點的四邊形是平行四邊形？若存在，請寫出所有符合條件的點F的坐標(biāo)；若不存在，請說明理由．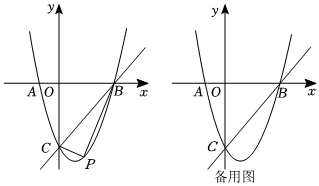
發(fā)布：2025/6/6 2:30:2組卷：615引用：5難度：0.1 -
2．如圖，拋物線y=x2-4x+3的圖象與坐標(biāo)軸交于A、B、C三點，
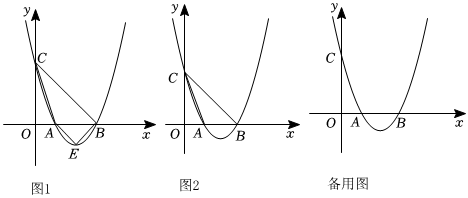
（1）求A、B兩點坐標(biāo)；
（2）如圖1，若拋物線的頂點為E，求△ABC與△ABE的面積之和；
（3）在拋物線上是否存在點P，使得∠ACB=∠PAB，若存在，求出點P坐標(biāo)，若不存在，請說明理由．發(fā)布：2025/6/6 5:0:1組卷：294引用：3難度：0.3 -
3．如圖，在平面直角坐標(biāo)系中，拋物線
與直線AB交于點A（0，-3），B（4，0）．y=34x2+bx+c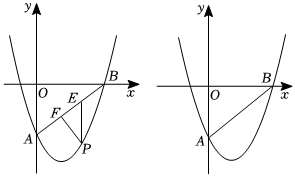
（1）求拋物線的函數(shù)解析式；
（2）點P是直線AB下方拋物線上一點，過點P作y軸的平行線，交AB于點E，過點P作AB的垂線，垂足為點F，求△PEF周長的最大值及此時點P的坐標(biāo)；
（3）在（2）中△PEF取得最大值的條件下，將該拋物線沿水平方向向左平移3個單位，點Q為點P的對應(yīng)點，點N為原拋物線對稱軸上一點．在平移后拋物線上確定一點M，使得以點B，Q，M，N為頂點的四邊形是平行四邊形，寫出所有符合條件的點M的坐標(biāo)，并寫出求解點M的坐標(biāo)的其中一種情況的過程．發(fā)布：2025/6/6 1:30:1組卷：517引用：5難度：0.1
相關(guān)試卷