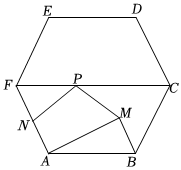
如圖，點M是邊長為2的正六邊形ABCDEF內的一點（不包括邊界），且AM⊥BM，P是FC上的一點，N是AF的中點，則PN+PM的最小值為（ ）
【考點】正多邊形和圓；軸對稱-最短路線問題．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/23 10:0:1組卷：393引用：4難度：0.4
相似題
-
1．拓展課上，同學們準備用卡紙做一個底面為邊長為10cm的正六邊形，高為6cm的無蓋包裝盒，它的表面展開圖如圖1所示．
（1）若選用長方形卡紙按圖2方式剪出包裝盒的表面展開圖，則AB的長為 cm；
（2）若選用一塊等邊三角形卡紙按圖3方式剪出包裝盒表面展開圖，則這個等邊三角形的邊長為 cm.
發布：2025/5/24 5:0:1組卷：96引用：1難度：0.5 -
2．若一個圓內接正六邊形的邊長是4cm,則這個正六邊形的邊心距=．
發布：2025/5/24 4:30:1組卷：296引用：6難度：0.5 -
3．一個邊長為3的正多邊形，每個外角均為45°，則該正多邊形的周長為 ．
發布：2025/5/24 8:30:1組卷：200引用：4難度：0.6