閱讀與理解：如圖1，等邊△BDE（邊長為a）按如圖所示方式設置．
操作與證明：
（1）操作：固定等邊△ABC（邊長為b），將△BDE繞點B按逆時針方向旋轉120°，連接AD，CE，如圖2；在圖2中，請直接寫出線段CE與AD之間具有怎樣的大小關系．
（2）操作：若將圖1中的△BDE，繞點B按逆時針方向旋轉任意一個角度α（60°＜α＜180°），連接AD，CE，AD與CE相交于點M，連BM，如圖3；在圖3中線段CE與AD之間具有怎樣的大小關系？∠EMD的度數是多少？證明你的結論．
猜想與發現：
（3）根據上面的操作過程，請你猜想在旋轉過程中，當α為多少度時，線段AD的長度最大，最大是多少？當α為多少度時，線段AD的長度最小，最小是多少？
?
【考點】幾何變換綜合題．
【答案】（1）EC=AD；
（2）EC=AD，∠EMD=60°；
（3）當α為180°時，線段AD的長度最大，等于a+b；當α為0°（或360°）時，線段AD的長度最小，等于a-b．
（2）EC=AD，∠EMD=60°；
（3）當α為180°時，線段AD的長度最大，等于a+b；當α為0°（或360°）時，線段AD的長度最小，等于a-b．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/2 14:0:2組卷：236引用：1難度：0.1
相似題
-
1．閱讀理解
圖1是邊長分別為a和b（a＞b）的兩個等邊三角形紙片ABC和C'DE疊放在一起（C與C'重合）的圖形．
操作與證明：
（1）操作：固定△ABC，將△C′DE繞點C按順時針方向旋轉30°，連接AD、BE，如圖2，在圖2中，線段BE與AD之間具有怎樣的大小關系？證明你的結論；
（2）若將圖1中的△C′DE繞點C按順時針方向任意旋轉一個角度α，連接AD、BE，如圖3，圖3中線段BE與AD之間具有怎樣的大小關系？證明你的結論；
猜想與發現：
（3）根據上面的操作和思考過程，請你猜想當α為 度時，線段AD的長度最大，當α為某個角度時，線段AD的長度最小，最小是 ．發布：2025/6/8 2:30:2組卷：36引用：2難度：0.3 -
2．如圖，兩個形狀，大小完全相同的含有30°、60°的三角板如圖放置，PA、PB與直線MN重合，且三角板PAC，三角板PBD均可以繞點P逆時針旋轉．
（1）①如圖1，∠DPC=度．
②我們規定，如果兩個三角形只要有一組邊平行，我們就稱這兩個三角形為“孿生三角形”，如圖1，三角板BPD不動，三角板PAC從圖示位置開始每秒10°逆時針旋轉一周（0°＜旋轉＜360°），問旋轉時間t為多少時，這兩個三角形是“孿生三角形”．
（2）如圖3，若三角板PAC的邊PA從PN外開始繞點P逆時針旋轉，轉速3°/秒，同時三角板PBD的邊PB從PM處開始繞點P逆時針旋轉，轉速2°/秒，在兩個三角板旋轉過程中，（PC轉到與PM重合時，兩三角板都停止轉動）．設兩個三角板旋轉時間為t秒，以下兩個結論：①為定值；②∠BPN+∠CPD為定值，請選擇你認為對的結論加以證明．∠CPD∠BPN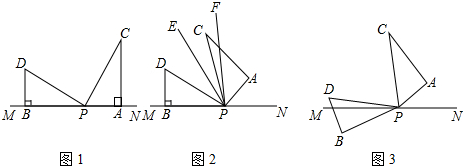
發布：2025/6/8 0:0:1組卷：1321引用：4難度：0.2 -
3．把△ABC繞著點A順時針旋轉α，得到△ADE．
（1）如圖1，當點D恰好在CB的延長線上時，若α=40°，求∠ADE的度數．
（2）如圖2，當點E恰好在CB的延長線上時，求證：EA平分∠DEC．
（3）如圖3，連接EB，如果BC=BE，連接CE與AD的延長線交于點F，直接寫出∠F的度數（用含α的式子表示）．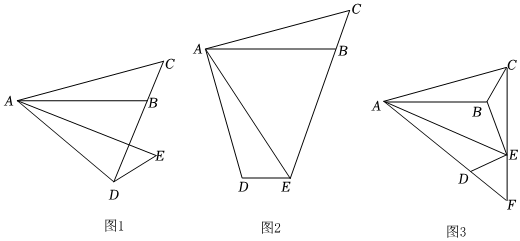
發布：2025/6/8 2:0:5組卷：6引用：1難度：0.1