有一塊三角形余料ABC，它的邊BC=90厘米，高AD=60厘米．要把它加工成正方形零件，使正方形的一邊在BC上，其余兩個頂點分別在AB，AC上．
（1）如圖1，請問加工成的正方形零件邊長是多少厘米？
（2）如圖2，如果所要加工成的零件是矩形，其它條件不變，請問矩形面積是否存在最大值？如果存在，請求出滿足最大值時矩形零件的兩條邊長．如果不存在，請說明理由．
（3）如圖3，如果所要加工成的零件是一個黃金矩形（寬長=5-12），請直接寫出這個黃金矩形的長和寬．（結果精確到0.1，5≈2.236）
寬
長
=
5
-
1
2
5
【答案】（1）36厘米；
（2）存在，面積達到最大時，矩形零件的兩條邊長分別為45厘米，30厘米；
（3）長為46.7厘米，寬為28.9厘米．
（2）存在，面積達到最大時，矩形零件的兩條邊長分別為45厘米，30厘米；
（3）長為46.7厘米，寬為28.9厘米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/27 6:0:3組卷：91引用：2難度：0.5
相似題
-
1．如圖，有一塊三角形余料ABC，BC=120mm,高線AD=80mm,要把它加工成一個矩形零件，使矩形的一邊在BC上，點P，M分別在AB，AC上，若滿足PM：PQ=3：2，則PM的長為（ ）發布：2025/6/1 2:0:5組卷：3220引用：7難度：0.5 -
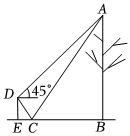2．小明和小麗想用所學知識測量一棵樹的高度AB，如圖，小麗先站在點E處觀測樹的頂端A，視線DA與水平線的夾角為45°；然后，小麗繼續站在E處，小明在小麗與樹之間的線段BE上放一平面鏡，經過不斷調整，當平面鏡放置在C處時，小麗剛好能在鏡子中看到樹的頂部A的像，這時測得CE=0.9m.已知小麗同學的眼睛到地面的距離DE=1.5m,點B、C、B在一條直線上，AB⊥BE，ED⊥BE，求這棵樹的高度AB．（平面鏡大小忽略不計）發布：2025/5/31 21:0:1組卷：55引用：2難度：0.6 -
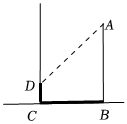3．如圖，在陽光下，旗桿AB在地面上的影長BC為14.4m；在建筑物墻面上的影長CD為3m.同一時刻，測得直立于地面長1m的木桿的影長為1.2m.求旗桿AB的高度．發布：2025/6/1 6:0:1組卷：64引用：1難度：0.6