問(wèn)題提出：（1）如圖①，在△ABC中，D、E分別是AB和AC的中點(diǎn)，連接DE，則DE與BC的數(shù)量關(guān)系是 DE=12BCDE=12BC，位置關(guān)系是 DE∥BCDE∥BC；
問(wèn)題探究：（2）如圖②，在四邊形ABCD中，∠BAC=90°，AB=AC=4，CD=2，E為AD中點(diǎn)，連接BE，求BE的最大值；
問(wèn)題解決：（3）如圖③，某小區(qū)計(jì)劃在一片足夠大的空地上修建四邊形的花園ABCD，其中BC=20米，AD=CD，AD⊥CD，AB∥CD，由于受地理位置的影響，∠ABC＜90°．根據(jù)要求，現(xiàn)計(jì)劃給該花園修建條筆直的綠色長(zhǎng)廊，且綠色長(zhǎng)廊的入口O定為BC的中點(diǎn)，出口定為點(diǎn)D，為了盡可能地提高觀賞體驗(yàn)，要求綠色長(zhǎng)廊OD最長(zhǎng)，試求綠色長(zhǎng)廊OD最長(zhǎng)為多少米？
1
2
1
2
【考點(diǎn)】四邊形綜合題．
【答案】DE=BC；DE∥BC
1
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/4 8:0:9組卷：270引用：2難度：0.3
相似題
-
1．已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=BC．
（1）如圖1．連接BD，若∠BAD=90°，求證：AD=CD．
（2）如圖2，點(diǎn)P，Q分別在線段AD，DC上，滿足PQ=AP+CQ，求證：∠PBQ=∠ABP+∠QBC；
（3）若點(diǎn)Q在DC的延長(zhǎng)線上，點(diǎn)P在DA的延長(zhǎng)線上，如圖3所示，仍然滿足PQ=AP+CQ，請(qǐng)寫(xiě)出∠PBQ與∠ADC的數(shù)量關(guān)系，并給出證明過(guò)程．
發(fā)布：2025/6/3 0:0:1組卷：434引用：2難度：0.3 -
2．（1）問(wèn)題發(fā)現(xiàn)：如圖①，正方形AEFG的兩邊分別在正方形ABCD的邊AB和AD上，連接CF．
①寫(xiě)出線段CF與DG的數(shù)量關(guān)系 ；
②寫(xiě)出直線CF與DG所夾銳角的度數(shù) ．
（2）拓展探究：
如圖②，將正方形AEFG繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)，在旋轉(zhuǎn)的過(guò)程中，（1）中的結(jié)論是否仍然成立？請(qǐng)利用圖②進(jìn)行說(shuō)明．
（3）問(wèn)題解決
如圖③，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O為AC的中點(diǎn)．點(diǎn)D在直線BC上運(yùn)動(dòng)，連接OE，則在點(diǎn)D的運(yùn)動(dòng)過(guò)程中，求線段OE的長(zhǎng)的最小值．（直接寫(xiě)出結(jié)果）
發(fā)布：2025/6/2 23:30:2組卷：143引用：1難度：0.1 -
3．探究：如圖①，在△ABC中，∠BAC=90°，AB=AC，直線m經(jīng)過(guò)點(diǎn)A，BD⊥m于點(diǎn)D，CE⊥m于點(diǎn)E，求證：△ABD≌△CAE．
應(yīng)用：如圖②，在△ABC中，AB=AC，D、A、E三點(diǎn)都在直線m上，并且有∠BDA=∠AEC=∠BAC．
求出DE、BD和CE的關(guān)系．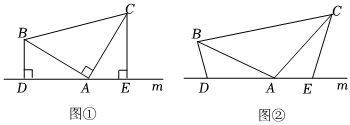
拓展：如圖①中，若DE=10．梯形BCED的面積 ．發(fā)布：2025/6/3 1:0:1組卷：94引用：1難度：0.4