綜合與實踐
問題情境：數學活動課上，老師組織同學們以“矩形”為主題開展數學活動．
已知矩形ABCD（AD＞AB）的一條對稱軸分別交邊AB、CD于點E、F，如圖①，奮進小組進行了如下的操作：以點B為圓心，BA的長為半徑作弧，交邊BC于點Q，已知點A'在弧AQ上運動（含A、Q兩點），連接BA′，再分別以點A、A'為圓心，大于12AA′的長為半徑作弧，兩弧相交于點G，作射線BG交AD于點H．
提出問題：
（1）如圖②，當點A'運動到EF上時，求∠ABH的度數；
拓展應用：
（2）如圖③，勤奮小組在圖②的基礎上進行如下操作：連接HA'并延長交BC于點P，請判斷△HBP的形狀，并說明理由；
解決問題：
（3）創新小組在圖③的基礎上進行如下操作：延長BA'交邊AD于點M，當△MPC是直角三角形時，請直接寫出矩形的邊BC和AB之間的數量關系．
1
2
AA
′
【考點】圓的綜合題．
【答案】（1）30°；（2）△HBP是等邊三角形；理由見解析；（3）BC=AB或BC=2AB．
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：558引用：4難度：0.3
相似題
-
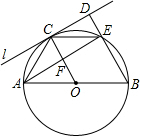1．如圖，AB為⊙O的直徑，C為半圓上一動點，過點C作⊙O的切線l,過點B作BD⊥l,垂足為D，BD與⊙O交于點E，連接OC，CE，AE，AE交OC于點F．
（1）求證：△CDE≌△EFC；
（2）若AB=4，連接AC．
①當AC=時，四邊形OBEC為菱形；
②當AC=時，四邊形EDCF為正方形．發布：2025/5/23 23:30:1組卷：963引用：8難度：0.5 -
2．如圖①，已知⊙O是△ABC的外接圓，∠ABC=∠ACB=α（45°＜α＜90°，D為
上一點，連接CD交AB于點E．?AB
（1）連接BD，若∠CDB=40°，求α的大小；
（2）如圖②，若點B恰好是中點，求證：CE2=BE?BA；?CD
（3）如圖③，將CD分別沿BC、AC翻折得到CM、CN，連接MN，若CD為直徑，請問是否為定值，如果是，請求出這個值，如果不是，請說明理由．ABMN
發布：2025/5/23 23:30:1組卷：1566引用：4難度：0.3 -
3．【問題提出】
（1）如圖①，在Rt△ABC中，∠A=90°，AB=3，AC=4，點D是邊BC上一動點，DE⊥AB于點E，DF⊥AC于點F，則EF的最小值為 ．
【問題探究】
（2）如圖②，在△ABC中，∠A=45°，AB=4，AC=3，點D是BC邊上一動點，DE⊥AB于點E，DF⊥AC于點F，⊙O是四邊形AEDF的外接圓，求⊙O直徑的最小值．2
【問題解決】
（3）某小區內有一塊形狀為四邊形的空地，如圖③所示，在四邊形ABCD中，AD∥BC，∠C=90°，∠B=60°，AD=200米，AB=4003米，點E在CD上，且CE=2DE，F、G分別是邊AB、BC上的兩個動點，且∠FEG=60°．為了改善人居環境，小區物業準備在盡可能大的四邊形BFEG區域內種植花卉，請問這個四邊形BFEG區域的面積是否存在最大值？若存在，求出面積的最大值；若不存在，請說明理由．3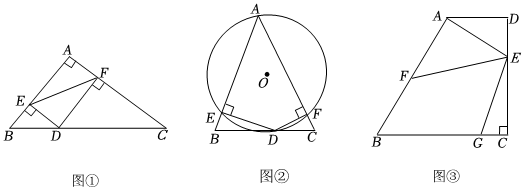
發布：2025/5/24 0:30:1組卷：570引用：3難度：0.1