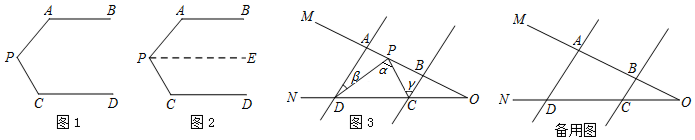
（1）問題情境：如圖1，AB∥CD，∠PAB=120°，∠PCD=130°，求∠APC的度數．
小辰的思路是：如圖2，過點P作PE∥AB，通過平行線的性質，可求得∠APC的度數．請寫出具體求解過程．
（2）問題遷移：
①如圖3，AD∥BC，點P在射線OM上運動，當點P在A、B兩點之間運動時，設∠CPD=∠α，∠ADP=∠β，∠BCP=∠γ，問：∠α、∠β、∠γ之間有何數量關系？請說明理由．
②在①的條件下，如果點P不在A、B兩點之間運動時（點P與點A、B、O三點不重合），請你直接寫出∠α、∠β、∠γ間的數量關系．
【考點】平行線的性質．
【答案】（1）110°．
（2）①∠α=∠β+∠γ，理由見解答；②∠α=|∠β-∠γ|．
（2）①∠α=∠β+∠γ，理由見解答；②∠α=|∠β-∠γ|．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：578引用：5難度：0.5
相似題
-
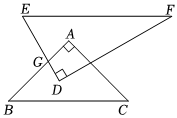1．如圖擺放的一副學生用直角三角板，∠F=30°，∠C=45°，AB與DE相交于點G，當EF∥BC時，∠EGB的度數是（ ）發布：2025/6/2 20:0:2組卷：148引用：1難度：0.5 -
2．已知，AB∥CD，直線FE交AB于點E，交CD于點F，點M在線段EF上，過M作射線MR、MP分別交射線AB、CD于點N、Q．
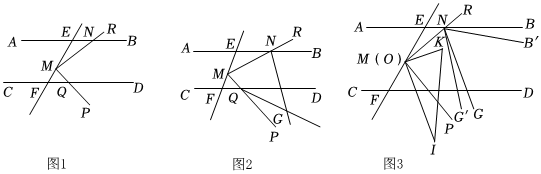
（1）如圖1，當MR⊥MP時，求∠MNB+∠MQD的度數；
（2）如圖2，若∠DQP和∠MNB的角平分線交于點G，求∠NMQ和∠NGQ的數量關系；
（3）如圖3，當MR⊥MP，且∠EFD=60°，∠EMR=20°時，作∠MNB的角平分線NG．把一三角板OKI的直角頂點O置于點M處，兩直角邊分別與MR和MP重合，將其繞點O點順時針旋轉，速度為5°每秒，當OI落在MF上時，三角板改為以相同速度逆時針旋轉．三角板開始運動的同時∠BNG繞點N以3°每秒的速度順時針旋轉，記旋轉中的∠BNG為∠B'NG'，當NG'和NA重合時，整個運動停止．設運動時間為t秒，當∠B'NG'的一邊和三角板的一直角邊互相平行時，請直接寫出t的值．發布：2025/6/2 20:0:2組卷：1683引用：2難度：0.2 -
3．如圖，已知AE∥BD，∠1=130°，∠2=30°，則∠C=．發布：2025/6/2 20:30:1組卷：1784引用：11難度：0.7