概念生成：定義：我們把經過三角形的一個頂點并與其對邊所在直線相切的圓叫做三角形的“切接圓”，如圖1，△ABC，⊙O經過點A，并與點A的對邊BC相切于點D，則該⊙O就叫做△ABC的切接圓．根據上述定義解決下列問題：
理解應用
（1）已知，Rt△ABC中，∠BAC=90°，AB=6，BC=10．
①如圖2，若點D在邊BC上，CD=254，以D為圓心，BD長為半徑作圓，則⊙D是△ABC的“切接圓”嗎？請說明理由．
②在圖3中，若點D在△ABC的邊上，以D為圓心，CD長為半徑作圓，當⊙D是Rt△ABC的“切接圓”時，求⊙D的半徑（直接寫出答案）．
思維拓展
（2）如圖4，△ABC中，AB=12．AC=BC=10，把△ABC放在平面直角坐標系中，使點C落在y軸上，邊AB落在x軸上．試說明：以拋物線y=116x2+4圖象上任意一點為圓心都可以作過點C的△ABC的“切接圓”．
25
4
1
16
x
2
【考點】圓的綜合題．
【答案】（1）①是，理由見解答部分；
②圓D的半徑為或4或；
（2）理由見解答部分．
②圓D的半徑為
40
9
15
4
（2）理由見解答部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/28 8:0:9組卷：1023引用：4難度：0.2
相似題
-
1．已知：△ABC內接于⊙O，連接OA，點D在⊙O上，連接AD，交BC于點E，∠CAD=∠BAO．
（1）如圖1，求證：AD⊥BC；
（2）如圖2，過點D作DF⊥AB于點F，交BC于點G，求證：CD=DG；
（3）如圖3，在（2）的條件下，若2∠BAD-∠ADB=3∠CAD，2AE=3DE，AC=1，求線段OA的長．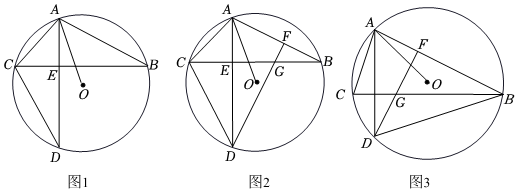
發布：2025/5/26 8:30:1組卷：271引用：2難度：0.1 -
2．在平面直角坐標系xOy中，點P坐標為（2，3），點Q為圖形M上一點，我們將線段PQ長度的最大值與最小值之間的差定義為點P視角圖形M的“寬度”．
（1）如圖，⊙O半徑為2，與x軸交于點A、B．
①在點P視角下，⊙O的“寬度”為 ，線段AB的“寬度”為 ；
②點G（m,0）為x軸上一點，若在點P視角下，線段AG的“寬度”為2，求m的取值范圍；
（2）⊙C的圓心在x軸上，且半徑為r,（r＞0），一次函數y=-x+233與x軸，y 軸分別交于點D，E．若線段DE上存在點K，使得在點K視角下，⊙C的“寬度”可以為2，求圓心C的橫坐標xC的取值范圍．3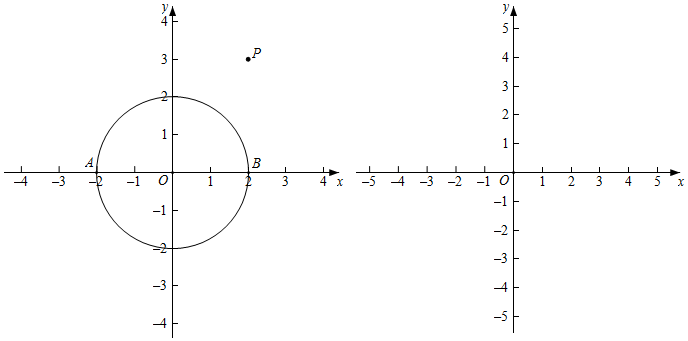
發布：2025/5/26 9:0:1組卷：181引用：1難度：0.3 -
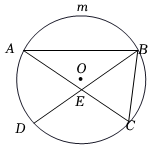3．如圖，點D是△ABC的外接圓⊙O上一點，且=?AD=?BC12，連接BD交AC于點E，?AmB
（1）求證AC=BD；
（2）若BD平分∠ABC，BC=1，求BD的長；
（3）已知圓心O在△ABC內部（不包括邊上），⊙O的半徑為5．
①若AB=8，求△ABC的面積；
②設=x,BC?AC=y,求y關于x的函數關系式，并求出y的取值范圍．BDBE發布：2025/5/26 9:0:1組卷：285引用：1難度：0.3