綜合與實踐
問題背景：
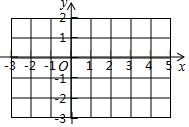
（1）已知A（1，2），B（3，2），C（1，-1），D（-3，-3）．在平面直角坐標系中描出這幾個點，并分別找到線段AB和CD中點P1、P2，然后寫出它們的坐標，則P1（2，2）（2，2），P2（-1，-2）（-1，-2）．
探究發現：
（2）結合上述計算結果，你能發現若線段的兩個端點的坐標分別為（x1，y1），（x2，y2），則線段的中點坐標為（x1+x22，y1+y22）（x1+x22，y1+y22）．
拓展應用：
（3）利用上述規律解決下列問題：已知三點E（-1，2），F（3，1），G（1，4），第四個點H（x,y）與點E、點F、點G中的一個點構成的線段的中點與另外兩個端點構成的線段的中點重合，求點H的坐標．
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
【考點】規律型：點的坐標．
【答案】（2，2）；（-1，-2）；
（
x
1
+
x
2
2
，
y
1
+
y
2
2
）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/14 8:0:9組卷：2647引用：13難度：0.5
相似題
-
1．如圖，在平面直角坐標系中，有若干個整數點（縱橫坐標都是整數的點），其順序按圖中“→”方向排列如（1，0），（2，0），（2，1），…根據這個規律探索可得，第100個點的坐標為．發布：2025/5/25 11:0:2組卷：1075引用：4難度：0.4 -
2．如圖，在平面直角坐標系上有點A（1，0），點A第一次跳動至點A1（-1，1），第二次點A1跳動至點A2（1，1），第三次點A2跳動至點A3（-2，2），第四次點A3跳動至點A4（2，2），……依此規律跳動下去，則點A2021與點A2022之間的距離是（ ）發布：2025/5/25 11:30:2組卷：135引用：2難度：0.6 -
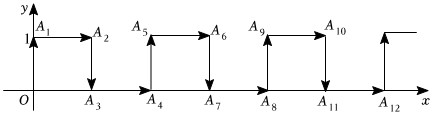
3．在平面直角坐標系中，一螞蟻從原點O出發，按向上、向右、向下、向右的方向依次不斷移動，每次移動1個單位，其行走路線如圖所示．則點A2022的坐標是 ．
發布：2025/5/25 3:0:2組卷：65引用：2難度：0.6