勾股定理是人類最偉大的十個科學發現之一，西方國家稱之為畢達哥拉斯定理．在我國古書《周髀算經》中就有“若勾三，股四，則弦五”的記載，我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”（如圖1），后人稱之為“趙爽弦圖”，流傳至今．
（1）①勾股定理的證明，人們已經找到了400多種方法，請從下列幾種常見的證明方法中任選一種來證明該定理（以下圖形均滿足證明勾股定理所需的條件）；
②如圖1，大正方形的面積是17，小正方形的面積是5，如果將如圖1中的四個全等的直角三角形按如圖2的形式擺放，求圖2中最大的正方形的面積．
（2）如圖4、5、6，以直角三角形的三邊為邊或直徑，分別向外部作正方形、半圓、等邊三角形，這三個圖形中面積關系滿足S1+S2=S3的有 33個；
（3）如圖7所示，分別以直角三角形三邊為直徑作半圓，設圖中兩個月形圖案（圖中陰影部分）的面積分別為S1、S2，直角三角形面積為S3，請判斷S1、S2、S3的關系 S1+S2=S3S1+S2=S3．
【考點】勾股定理的證明．
【答案】3；S1+S2=S3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 3:0:1組卷：615引用：3難度：0.6
相似題
-
1．【教材呈現】如圖是華師版八年級上冊124頁的部分內容．
【證明定理】如圖，它由2個全等的直角三角形與一個小直角梯形組成，恰好拼成一個大直角梯形，也能證明勾股定理，請你寫出證明過程．勾股定理的“無字證明”
在勾股定理的學習過程中，我們已經學會了運用以下圖形，驗證著名的勾股定理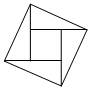
這種根據圖形直觀推論或驗證數學規律和公式的方法，簡稱為“無字證明”，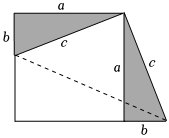
發布：2025/6/2 10:0:2組卷：466引用：1難度：0.2 -
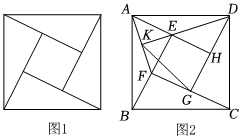2．如圖1，四個全等的直角三角形圍成一個大正方形，中間是個小正方形，這個圖形是我國漢代趙爽在注解《周髀算經》時給出的，人們稱它為“趙爽弦圖”．在弦圖中（如圖2）連結AF，DE，并延長DE交AF于點K，連結KG．若AH=2DH=，則KG的長為（ ）22發布：2025/6/1 1:30:1組卷：531引用：5難度：0.6 -
3．我們發現，用不同的方式表示同一圖形的面積可以解決線段長度之間關系的有關問題，這種方法稱為等面積法，這是一種重要的數學方法，請你用等面積法來探究下列兩個問題：
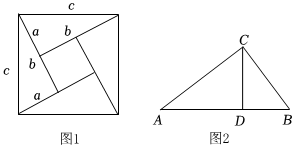
（1）如圖1是著名的“趙爽弦圖”，由四個全等的直角三角形拼成，請你用它驗證勾股定理；
（2）如圖2，在Rt△ABC中∠ACB=90°，CD是AB邊上高，AC=12，BC=5，求CD的長度．發布：2025/6/1 19:0:6組卷：519引用：1難度：0.6