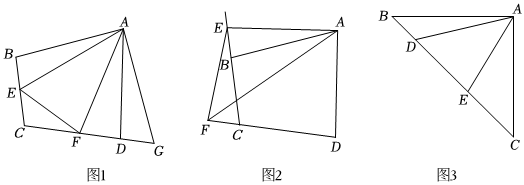
如圖1，在四邊形ABCD中，AB=AD，∠B+∠ADC=180°，點E，F分別變到四邊形ABCD的邊BC，CD上，∠EAF=12∠BAD，連接EF．
（1）思路梳理：將△ABE繞點A逆時針旋轉至△ADG，如圖1，使AB與AD重合，由∠B+∠ADC=180°，得∠FDG=180°，即點F，D，G三點共線．易證△AFG≌△AFE，故EF，BE，DF之間的數量關系為 EF=BE+DFEF=BE+DF；
（2）類比引申：如圖2，在圖1的條件下，若點E，F由原來的位置分別變到四邊形ABC的邊CB，DC的延長線上，連接EF，試猜想EF，BE，DF之間的數量關系，并給出證明；
（3）聯想拓展：如圖3，在△ABC中，∠BAC=90°，AB=AC，點D，E均在邊BC上，且∠DAE=45°，若BD=1，EC=2，求DE的長．
∠
EAF
=
1
2
∠
BAD
【考點】四邊形綜合題．
【答案】EF=BE+DF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：172引用：1難度：0.5
相似題
-
1．在菱形ABCD中，∠ABC是銳角，E是BC邊上的動點，將射線AE繞點A按逆時針方向旋轉，交直線CD于點F．
（1）如圖1，當AE⊥BC，∠EAF=∠ABC時．
①求證：△AEB≌△AFD；
②連結BD，EF，若=EFBD，菱形ABCD的邊長為6，求△ABE的面積；23
（2）如圖2，當∠EAF=∠BAD時，延長BC交射線AF于點M，延長DC交射線AE于點N，連結AC，MN，若AB=5，AC=3，則當CE為何值時，AM=MN？12
發布：2025/6/12 23:30:2組卷：79引用：1難度：0.2 -
2．已知△ABC中，AB=AC=5，BC=8，點D為BC中點，連結AD．一動點P從點A出發，沿折線AB-BD向終點D運動，在AB邊上以每秒5個單位長度的速度運動，在BD邊上以每秒2個單位長度的速度運動，連結PD，以PA、PD為鄰邊構造平行四邊形APDQ．設運動時間為t秒．（t＞0）．
（1）tanB=．
（2）用含t的代數式表示線段BP的長．
（3）當平行四邊形APDQ與△ABC重疊部分圖形是軸對稱圖形時，求t的值．
（4）當0＜t＜3時，平行四邊形APDQ被△ABC的邊分成兩部分圖形的面積比為1：7時，直接寫出t的值．
發布：2025/6/12 23:30:2組卷：68引用：1難度：0.3 -
3．如圖，在Rt△ABC中，∠BAC=90°，AB=4，AC=25，動點P從點C出發以每秒1個單位長度的速度沿CB向終點B運動（點P不與點B、C重合），以CP為邊在BC上方作等腰Rt△CPN，使∠CPN=90°，CP=NP，以CP，CN為鄰邊作平行四邊形CPMN，點P的運動時間為t秒．5
（1）NP的長為 ，點M到BC的距離為 ．（用含t的代數式表示）
（2）當點M在邊AB上時，求CN的長．
（3）當點M在△ABC一邊垂直平分線上時，求t的值．
（4）作點B關于直線PM的對稱點B'，點Q為AC的中點，連結B'Q，當B'Q與△ABC的邊垂直時，直接寫出t的值．發布：2025/6/12 22:30:1組卷：116引用：2難度：0.1