婆羅摩芨多是公元7世紀(jì)古印度偉大的數(shù)學(xué)家，他在三角形、四邊形、零和負(fù)數(shù)的運(yùn)算規(guī)則，二次方程等方面均有建樹(shù)，他也研究過(guò)對(duì)角線互相垂直的圓內(nèi)接四邊形，我們把這類對(duì)角線互相垂直的圓內(nèi)接四邊形稱為“婆氏四邊形”；
（1）若平行四邊形ABCD是“婆氏四邊形”，則四邊形ABCD是 ③③．（填序號(hào)）
①矩形②菱形③正方形
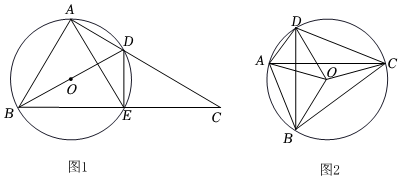
（2）如圖1，Rt△ABC中，∠BAC=90°，以AB為弦的⊙O交AC于D，交BC于E，連接DE、AE、BD，AB=6，sinC=35，若四邊形ABED是“婆氏四邊形”，求DE的長(zhǎng)；
（3）如圖2，四邊形ABCD為⊙O的內(nèi)接四邊形，連接AC，BD，OA，OB，OC，OD，已知∠BOC+∠AOD=180°，
①求證：四邊形ABCD是“婆氏四邊形”；
②當(dāng)AD+BC=4時(shí)，求⊙O半徑的最小值．
sin
C
=
3
5
【考點(diǎn)】圓的綜合題．
【答案】③
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：1199引用：2難度：0.1
相似題
-
1．問(wèn)題提出：
（1）我國(guó)古代數(shù)學(xué)家趙爽巧妙地用“弦圖”證明了勾股定理，標(biāo)志著中國(guó)古代的數(shù)學(xué)成就．小林用邊長(zhǎng)為10的正方形ABCD制作了一個(gè)“弦圖”：如圖①，在正方形ABCD內(nèi)取一點(diǎn)E，使得∠BEC=90°，作DF⊥CE，AG⊥DF，垂足分別為F、G，延長(zhǎng)BE交AG于點(diǎn)H．若EH=2，求tan∠BCE；
問(wèn)題解決：
（2）如圖②，四邊形ABCD是公園中一塊空地，AB=BC=50米，AD=CD，∠ABC=90°，∠D=60°，空地中有一段半徑為50米的弧形道路（即），現(xiàn)準(zhǔn)備在?AC上找一點(diǎn)P，將弧形道路改造為三條直路（即PA、PB、PC），并要求∠BPC=90°，三條直路將空地分割為△ABP、△BCP和四邊形APCD三個(gè)區(qū)域，用來(lái)種植不同的花草．?AC
①求∠APC的度數(shù)；
②求四邊形APCD的面積．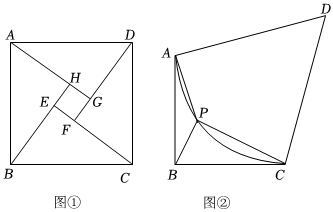
發(fā)布：2025/5/23 4:30:1組卷：429引用：1難度：0.3 -
2．已知AB是⊙O的直徑，弦CD⊥AB，垂足為點(diǎn)H，點(diǎn)E在直徑AB上（與A、B不重合），EH=AH，連接CE并延長(zhǎng)與⊙O交于點(diǎn)F．
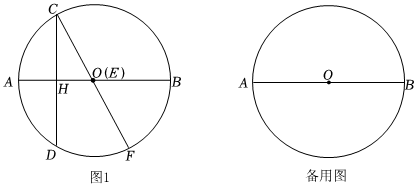
（1）如圖1，當(dāng)點(diǎn)E與點(diǎn)O重合時(shí)，求∠AOC的度數(shù)；
（2）連接AF交弦CD于點(diǎn)P，如果，求CEEF=43的值；DPCP
（3）當(dāng)四邊形ACOF是梯形時(shí)，且AB=6，求AE的長(zhǎng)．發(fā)布：2025/5/23 5:0:2組卷：540引用：1難度：0.3 -
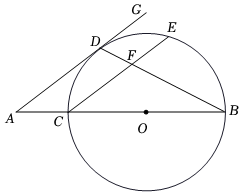3．如圖，已知BC為⊙O的直徑，點(diǎn)D為的中點(diǎn)，過(guò)點(diǎn)D作DG∥CE，交BC的延長(zhǎng)線于點(diǎn)A，連接BD，交CE于點(diǎn)F．?CE
（1）求證：AD是⊙O的切線；
（2）若EF=3，CF=5，tan∠GDB=2，求AC的長(zhǎng)．發(fā)布：2025/5/23 5:0:2組卷：1251引用：3難度：0.5