2023年浙江省嘉興市上海外國語大學秀洲外國語學校中考數學二模試卷

一、選擇題（本題有10小題．每小題3分，共30分．每小題只有一個選項是正確的．不選、多選、錯選，均不給分）

• 1．計算：（-2）+3的結果是（　　）

  A．-5

  B．-1

  C．1

  D．5
  組卷：729引用：26難度：0.9

  解析

• 2．為了了解家里的用水情況，以便能更好的節約用水，小方把自己家1至6月份的用水量繪制成如圖的折線圖，那么小方家這6個月的月用水量最大是（　　）

  A．1月

  B．4月

  C．5月

  D．6月
  組卷：391引用：10難度：0.9

  解析

• 3．如圖所示的幾何體由一個圓柱體和一個長方體組成，它的主視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：143引用：11難度：0.9

  解析

• 4．下列計算正確的是（　　）

  A．a3+a2=2a5

  B．a3?a2=a6

  C．a3÷a2=a

  D．（a3）2=a9
  組卷：928引用：25難度：0.9

  解析

• 5．不等式組

  x + 1 ＞ 0

  x - 3 ＞ 0

  的解集是（　　）

  A．x＞-1

  B．x＞3

  C．-1＜x＜3

  D．x＜3
  組卷：996引用：16難度：0.9

  解析

• 6．若關于x的一元二次方程ax²-4x+1=0有兩個相等實數根，則a的值是（　　）

  A．-1

  B．1

  C．-4

  D．4
  組卷：124引用：9難度：0.7

  解析

• 7．某學習小組9名學生參加“生活中的數學知識競賽”，他們的得分情況如表：
  

  人數（人）	1	3	4	1
  分數（分）	80	85	90	95

  那么這9名學生所得分數的眾數和中位數分別是（　　）

  A．90，90

  B．90，85

  C．90，87.5

  D．85，85
  組卷：336引用：11難度：0.7

  解析

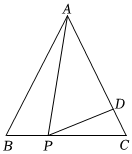• 8．如圖，在△ABC中，AB=AC=9，

  BP

  =

  1

  3

  BC

  =

  2

  ，D在AC上，且∠APD=∠B，則CD的長是（　　）

  A．2

  B． 9 8

  C． 4 3

  D． 8 9
  組卷：288引用：2難度：0.5

  解析

三、解答題（本題有8小題，共66分．解答需寫出必要的文字說明，演算步驟或證明過程）

• 23．某公司銷售一種進價為20元/個的計算器，其銷售量y（萬個）與銷售價格x（元/個）的變化如下表：
  

  價格x（元/個）	…	30	40	50	60	…
  銷售量y（萬個）	…	5	4	3	2	…

  同時，銷售過程中的其他開支（不含進價）總計40萬元．
  （1）觀察并分析表中的y與x之間的對應關系，用所學過的一次函數，反比例函數或二次函數的有關知識寫出y（萬個）與x（元/個）的函數解析式．
  （2）求出該公司銷售這種計算器的凈得利潤z（萬元）與銷售價格x（元/個）的函數解析式，銷售價格定為多少元時凈得利潤最大，最大值是多少？
  （3）該公司要求凈得利潤不能低于40萬元，請寫出銷售價格x（元/個）的取值范圍，若還需考慮銷售量盡可能大，銷售價格應定為多少元？
  組卷：2397引用：77難度：0.5

  解析

• 24．婆羅摩芨多是公元7世紀古印度偉大的數學家，他在三角形、四邊形、零和負數的運算規則，二次方程等方面均有建樹，他也研究過對角線互相垂直的圓內接四邊形，我們把這類對角線互相垂直的圓內接四邊形稱為“婆氏四邊形”；
  （1）若平行四邊形ABCD是“婆氏四邊形”，則四邊形ABCD是

  ．（填序號）
  ①矩形②菱形③正方形
  （2）如圖1，Rt△ABC中，∠BAC=90°，以AB為弦的⊙O交AC于D，交BC于E，連接DE、AE、BD，AB=6，

  sin

  C

  =

  3

  5

  ，若四邊形ABED是“婆氏四邊形”，求DE的長；
  （3）如圖2，四邊形ABCD為⊙O的內接四邊形，連接AC，BD，OA，OB，OC，OD，已知∠BOC+∠AOD=180°，
  ①求證：四邊形ABCD是“婆氏四邊形”；
  ②當AD+BC=4時，求⊙O半徑的最小值．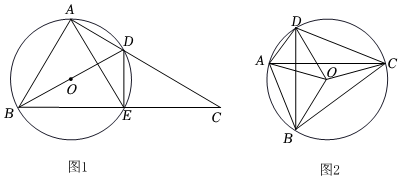
  
  組卷：1196引用：2難度：0.1

  解析