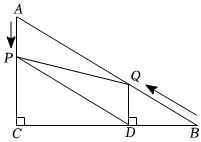
如圖，已知Rt△ABC中，∠C=90°，∠B=30°，AC=10，點(diǎn)P從點(diǎn)A出發(fā)，沿AC方向以每秒1個(gè)單位的速度向點(diǎn)C運(yùn)動(dòng)，點(diǎn)Q同時(shí)從點(diǎn)B出發(fā)，沿BA方向以每秒2個(gè)單位的速度向點(diǎn)A運(yùn)動(dòng)，設(shè)它們的運(yùn)動(dòng)時(shí)間為t秒（0＜t≤10），過點(diǎn)Q作QD⊥BC于點(diǎn)D，連接PQ，PD．
（1）求證：四邊形APDQ是平行四邊形；
（2）若四邊形APDQ是菱形，求t的值；
（3）當(dāng)t=5或85或8時(shí)，△PDQ是直角三角形．
【考點(diǎn)】四邊形綜合題．
【答案】5或8
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/14 8:0:9組卷：37引用：1難度：0.4
相似題
-
1．如圖直角坐標(biāo)系中直線AB與x軸正半軸、y軸正半軸交于A，B兩點(diǎn)，已知B（0，4），∠BAO=30°，P，Q分別是線段OB，AB上的兩個(gè)動(dòng)點(diǎn)，P從O出發(fā)以每秒3個(gè)單位長(zhǎng)度的速度向終點(diǎn)B運(yùn)動(dòng)，Q從B出發(fā)以每秒8個(gè)單位長(zhǎng)度的速度向終點(diǎn)A運(yùn)動(dòng)，兩點(diǎn)同時(shí)出發(fā)，當(dāng)其中一點(diǎn)到達(dá)終點(diǎn)時(shí)整個(gè)運(yùn)動(dòng)結(jié)束，設(shè)運(yùn)動(dòng)時(shí)間為t（秒）．
（1）求線段AB的長(zhǎng)，及點(diǎn)A的坐標(biāo)；
（2）t為何值時(shí)，△BPQ的面積為2；3
（3）若C為OA的中點(diǎn)，連接QC，QP，以QC，QP為鄰邊作平行四邊形PQCD，
①t為何值時(shí)，點(diǎn)D恰好落在坐標(biāo)軸上；
②是否存在時(shí)間t使x軸恰好將平行四邊形PQCD的面積分成1：3的兩部分，若存在，直接寫出t的值．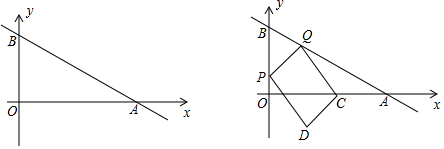
發(fā)布：2025/6/20 23:0:1組卷：1027引用：6難度：0.3 -
2．如圖，四邊形ABCD是正方形，E是線段BC上一點(diǎn)，連接AE，將AE繞點(diǎn)E順時(shí)針旋轉(zhuǎn)90°，得到EF，過點(diǎn)F作FG⊥CD于點(diǎn)G．
（1）如圖①，當(dāng)E是BC的中點(diǎn)時(shí)，請(qǐng)直接寫出線段FG和BE的數(shù)量關(guān)系；
（2）如圖②，當(dāng)E不是BC的中點(diǎn)時(shí)，（1）中的結(jié)論是否成立？請(qǐng)說明理由；
（3）若BC=4，CE=2，EF與CD交于點(diǎn)P，請(qǐng)求出CP的長(zhǎng)．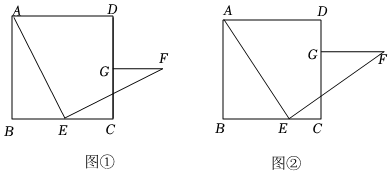
發(fā)布：2025/6/20 12:0:2組卷：32引用：1難度：0.1 -
3．如圖1，正方形ABCD，E為平面內(nèi)一點(diǎn)，且∠BEC=90°，把△BCE繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)90°得△BAG，直線AG和直線CE交于點(diǎn)F．
（1）證明：四邊形BEFG是正方形；
（2）若∠AGD=135°，猜測(cè)CE和CF的數(shù)量關(guān)系，并說明理由；
（3）如圖2，連接DF，若AB=13，CF=17，求DF的長(zhǎng)．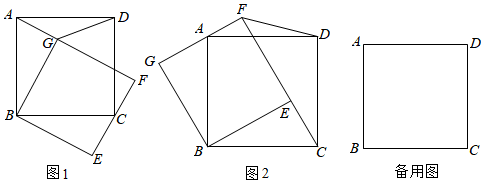
發(fā)布：2025/6/20 10:30:1組卷：97引用：1難度：0.1