 如圖,正方形ABCD的邊長為4,點M、N分別在AB、CD上.將該紙片沿MN折疊,使點D落在邊BC上的點E處,折痕MN與DE相交于Q.
如圖,正方形ABCD的邊長為4,點M、N分別在AB、CD上.將該紙片沿MN折疊,使點D落在邊BC上的點E處,折痕MN與DE相交于Q.
(1)請判斷DE與MN之間的數(shù)量關(guān)系,并說明理由;
(2)若點G為EF的中點,隨著折痕MN位置的變化,請求出△GQE周長的最小值.
【答案】(1)MN=DE;理由見解答;(2)△GQE周長的最小為2+.
2
5
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:141引用:2難度:0.3
相似題
-
 1.如圖,將一張矩形紙片沿著AE折疊后,點D恰好與BC邊上的點F重合,已知:AB=6,BC=10,則FC的長度為( )
1.如圖,將一張矩形紙片沿著AE折疊后,點D恰好與BC邊上的點F重合,已知:AB=6,BC=10,則FC的長度為( )A.1 B.2 C.3 D.4 發(fā)布:2025/6/7 4:0:1組卷:52引用:2難度:0.6 -
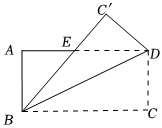 2.如圖,把一張矩形紙片ABCD沿對角線BD折疊,使C點落在C′,且BC′與AD交于E點,若∠ABE=40°,則∠ADB=.發(fā)布:2025/6/7 4:30:1組卷:475引用:19難度:0.7
2.如圖,把一張矩形紙片ABCD沿對角線BD折疊,使C點落在C′,且BC′與AD交于E點,若∠ABE=40°,則∠ADB=.發(fā)布:2025/6/7 4:30:1組卷:475引用:19難度:0.7 -
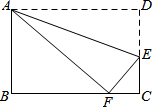 3.如圖,將矩形ABCD沿直線AE折疊,頂點D恰好落在BC邊上F處,已知CE=3,AB=8,求BF.發(fā)布:2025/6/7 4:0:1組卷:473引用:8難度:0.5
3.如圖,將矩形ABCD沿直線AE折疊,頂點D恰好落在BC邊上F處,已知CE=3,AB=8,求BF.發(fā)布:2025/6/7 4:0:1組卷:473引用:8難度:0.5


