問題提出：
如圖1，在Rt△ABC中AC=BC，∠ACB=90°，點D為AB上一點，連接CD，為探究AD2，BD2，CD2之間的數量關系，劉星同學思考后，提出以下解決方法．
探究解決：
將圖1中CD繞著點C順時針方向旋轉90°，得到CE，連接DE，AE，如圖2，請解決以下問題：
（1）證明：△ACE≌△BCD；
（2）證明：∠DAE=90°；
（3）直接寫出AD2，BD2，CD2之間的數量關系為 AD2+BD2=2CD2AD2+BD2=2CD2；
（4）拓展應用：如圖3，四邊形ABCD內接于⊙O，且BD為⊙O直徑，BC=DC，連接AC，若AB=5，BC=17，則AC=4242．
17
2
2
【考點】圓的綜合題．
【答案】AD2+BD2=2CD2；4
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：276引用：2難度：0.3
相似題
-
1．在平面直角坐標系xOy中，我們給出如下定義：將圖形M繞直線x=3上某一點P順時針旋轉90°，再關于直線x=3對稱，得到圖形N，我們稱圖形N為圖形M關于點P的二次關聯圖形．已知點A（0，1）．
（1）若點P的坐標是（3，0），直接寫出點A關于點P的二次關聯圖形的坐標 ；
（2）若點A關于點P的二次關聯圖形與點A重合，求點P的坐標（直接寫出結果即可）；
（3）已知⊙O的半徑為1，點A關于點P的二次關聯圖形在⊙O上且不與點A重合．若線段AB=1，其關于點P的二次關聯圖形上的任意一點都在⊙O及其內部，求此時P點坐標及點B的縱坐標yB的取值范圍．發布：2025/6/3 8:30:1組卷：844引用：4難度：0.1 -
2．在等邊△AOB中，將扇形COD按圖1擺放，使扇形的半徑OC，OD分別與OA，OB重合，OA=OB=2，OC=OD=1，固定等邊△AOB不動，讓扇形COD繞點O逆時針旋轉（即圖2旋轉方式），線段AC，BD也隨之變化，設旋轉角為α．（0＜α≤360°）
發現：（1）當OC∥AB時，旋轉角α=度；
（2）線段AC與BD的數量關系是 ；
應用：（3）當A，C，D三點共線時，求BD的長．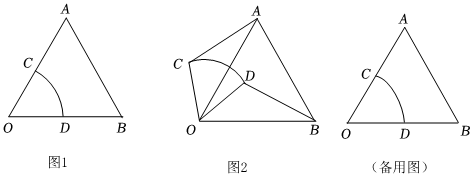
發布：2025/6/3 6:30:2組卷：30引用：2難度：0.2 -
3．如圖，在四邊形ABCD中，AD∥BC，AD⊥CD，AC=AB，⊙O為△ABC的外接圓．
（1）如圖1，求證：AD是⊙O的切線；
（2）如圖2，CD交⊙O于點E，過點A作AG⊥BE，垂足為F，交BC于點G．
①求證：AG=BG；
②若AD=2，CD=3，求FG的長．發布：2025/6/3 9:0:1組卷：1598引用：6難度：0.3