我們定義：如圖1，在△ABC看，把AB繞點A順時針旋轉α（0°＜α＜180°）得到AB'，把AC繞點A逆時針旋轉β得到AC'，連接B'C'．當α+β=180°時，我們稱△AB'C'是△ABC的“旋補三角形”，△AB'C'邊B'C'上的中線AD叫做△ABC的“旋補中線”，點A叫做“旋補中心”．
特例感知：
（1）在圖2，圖3中，△AB'C'是△ABC的“旋補三角形”，AD是△ABC的“旋補中線”．
①如圖2，當△ABC為等邊三角形時，AD與BC的數量關系為AD=1212BC；
②如圖3，當∠BAC=90°，BC=8時，則AD長為 44．
猜想論證：
（2）在圖1中，當△ABC為任意三角形時，猜想AD與BC的數量關系，并給予證明．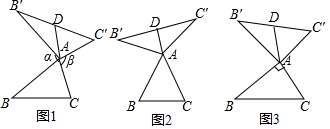
1
2
1
2
【考點】幾何變換綜合題．
【答案】；4
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：3285引用：12難度：0.3
相似題
-
1．綜合與探究
問題情境
如圖，在矩形紙片ABCD中，點E．F分別是邊AD，BC上的動點，連接EF，BE，DF．將矩形紙片ABCD分別沿直線BE，DF折疊，點A的對應點為點M，點C的對應點為點N．
操作探究
（1）如圖（1），若點F與點M重合，DN與EF交于點G，求證：DG=GM；
探究發現
（2）如圖（2），當點M，N落在對角線BD上時，判斷并證明四邊形BFDE的形狀；
探究拓廣
（3）當點M，N落在對角線AC上時．
①在圖（3）中補全圖形；
②若AB=2，AD=3，求△BEF的面積．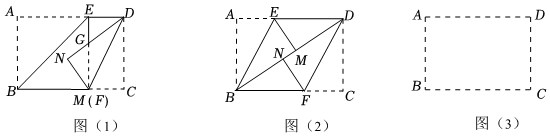
發布：2025/5/25 17:0:1組卷：557引用：2難度：0.4 -
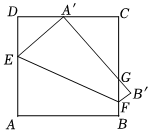2．如圖，正方形ABCD的邊長為8，點E，F分別在邊AD，BC上，將正方形沿EF折疊，使點A落在邊CD上的A'處，點B落在B'處，A'B'交BC于G．下列結論正確的是（ ）發布：2025/5/25 16:0:2組卷：116引用：2難度：0.2 -
3．折紙的思考．
【操作體驗】
用一張矩形紙片折等邊三角形．
第一步，對折矩形紙片ABCD（AB＞BC）（圖①），使AB與DC重合，得到折痕EF，把紙片展平（圖②）．
第二步，如圖③，再一次折疊紙片，使點C落在EF上的P處，并使折痕經過點B，得到折痕BG，折出PB、PC，得到△PBC．
（1）說明△PBC是等邊三角形．
【數學思考】
（2）如圖④，小明畫出了圖③的矩形ABCD和等邊三角形PBC．他發現，在矩形ABCD中把△PBC經過圖形變化，可以得到圖⑤中的更大的等邊三角形，請描述圖形變化的過程．
（3）已知矩形一邊長為3cm,另一邊長為a cm,對于每一個確定的a的值，在矩形中都能畫出最大的等邊三角形，請畫出不同情形的示意圖，并寫出對應的a的取值范圍．
【問題解決】
（4）用一張正方形鐵片剪一個直角邊長分別為4cm和1cm的直角三角形鐵片，所需正方形鐵片的邊長的最小值為cm.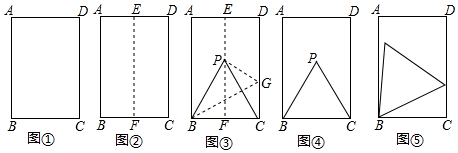
發布：2025/5/25 16:0:2組卷：3493引用：3難度：0.3