探究題．

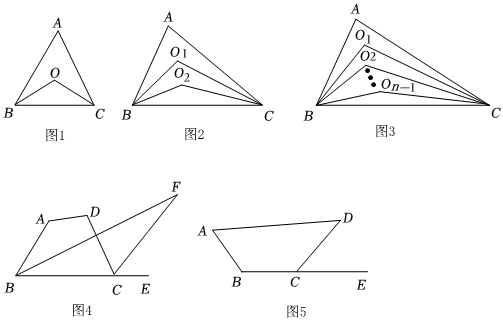
（1）若△ABC中，∠A=60°
①如圖1，若∠ABC和∠ACB的角平分線相交于點O，則∠BOC=

120°

120°

．
②如圖2，若∠ABC和∠ACB的三等分線相交于點O₁、O₂，則∠BO₁C=

100°

100°

．
（2）若△ABC中，∠A=x°
①如圖1，若∠ABC和∠ACB的角平分線相交于點O，則用x表示∠BOC=

（

90

+

1

2

x

）

（

90

+

1

2

x

）

度．
②如圖2，若∠ABC和∠ACB的三等分線相交于點O₁、O₂，則用x表示∠BO₁C=

（

60

+

2

3

x

）

（

60

+

2

3

x

）

度．
③如圖3，若∠ABC和∠ACB的n等分線相交于點O₁、O₂、……、O_n-1，則用x表示∠BO₁C=

（

180

n

+

n

-

1

n

x

）

（

180

n

+

n

-

1

n

x

）

度．（結果不需化簡）
（3）如圖，四邊形ABCD中，為四邊形ABCD的∠ABC的角平分線及外角∠DCE的平分線所在的直線構成的銳角：
①如圖4，若設∠A=140°，∠D=100°，則∠F=

30°

30°

．
②如圖5，若設∠A=60°，∠D=50°，請在圖中畫出∠F，則∠F=

35°

35°

．
③若設∠A=x°，∠D=y°，一定存在∠F嗎？如有，求出∠F的值（用x、y表示），如不一定，指出x、y滿足什么條件時，不存在∠F，并說明理由．