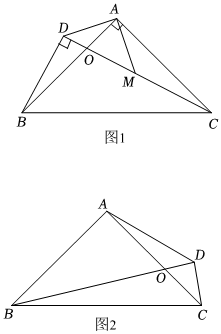
如圖，在Rt△ABC中，∠BAC=90°，AB=AC，在BC的同側作任意Rt△DBC，∠BDC=90°．
（1）若CD=2BD，M是CD中點（如圖1），求證：AD=AM；
下面是小明的證明過程，請你將它補充完整：
證明：設AB與CD相交于點O，
∵∠BDC=90°，∠BAC=90°，
∴∠DOB+∠DBO=∠AOC+∠ACO=90°．
∵∠DOB=∠AOC，
∴∠DBO=∠MCAMCA．
∵M是DC的中點，CD=2BD，
∴CM=12CD=BDBD．
又∵AB=AC，
∴△ADB≌△AMC．
∴AD=AM．
（2）若CD＜BD（如圖2），在BD上是否存在一點N，使得△ADN是以DN為斜邊的等腰直角三角形？若存在，請在圖2中確定點N的位置，并加以證明；若不存在，請說明理由；
（3）當CD≠BD時，線段AD，BD與CD滿足怎樣的數量關系？請直接寫出．
1
2
【考點】三角形綜合題．
【答案】MCA；BD
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/17 8:0:9組卷：40引用：1難度：0.3
相似題
-
1．已知，如圖，在平面直角坐標系中，A為y軸正半軸上一點，B為x軸負半軸上一點．
（1）若BP平分∠ABO，AP平分∠BAO的外角，求∠P．
（2）如圖2，C為x軸正半軸上一點，BP平分∠ABC，且P在AC的垂直平分線上．若∠ABC=2∠ACB，求證：AP∥BC．
（3）在第（2）問的條件下，D是AB上一點，E是x軸正半軸上一點，連AE交DP于H．當∠DHE與∠ABE滿足什么條件時，DP=AE，請說明理由．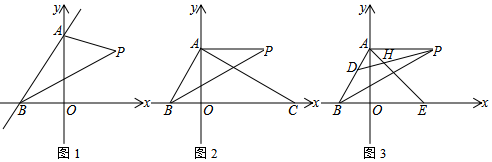
發布：2025/6/17 19:30:1組卷：75引用：1難度：0.3 -
2．把一副三角板按如圖1擺放（點C與點E重合），點B，C（E），F在同一直線上．∠ACB=∠DFE=90°，∠A=30°，∠DEF=45°，BC=EF=8cm,點P是線段AB的中點．△DEF從圖1的位置出發，以4cm/s的速度沿CB方向勻速運動，如圖2，DE與AC相交于點Q，連接PQ．當點D運動到AC邊上時，△DEF停止運動．設運動時間為t（s）．
（1）當t=1時，求AQ的長；
（2）當t為何值時，點A在線段PQ的垂直平分線上？
（3）當t為何值時，△APQ是直角三角形？
發布：2025/6/17 21:30:1組卷：286引用：3難度：0.1 -
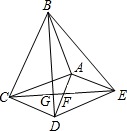3．如圖，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，連接CE交AD于點F，連接BD交CE于點G，連接BE．下列結論中，正確的結論有（ ）
①CE=BD；
②△ADC是等腰直角三角形；
③∠ADB=∠AEB；
④S四邊形BCDE=BD?CE；12
⑤BC2+DE2=BE2+CD2．發布：2025/6/18 15:30:1組卷：1902引用：10難度：0.7