當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省達州市達川區百節中心學校八年級（下）期末數學試卷

發布：2024/7/18 8:0:9

1．下列電視臺的臺標，是中心對稱圖形的是（　　）
A． B． C． D．
組卷：158引用：22難度：0.8
解析
2．不等式x＞1的解集在數軸上表示正確的是（　　）
A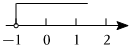． B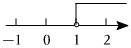． C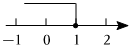． D．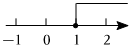
組卷：72引用：4難度：0.9
解析
3．下列各式中，能用完全平方公式分解因式的是（　　）
A．4x²-4x+1 B．6x²+3x+1 C．x²+4xy+2y² D．9x²+18x+1
組卷：342引用：3難度：0.8
解析
4．如圖，在△ABC中，AB=AC，∠A=120°，BC=6cm,AB的垂直平分線交BC于點M，交AB于點E，AC的垂直平分線交BC于點N，交AC于點F，則MN的長為（　　）
A．4cm B．3cm C．2cm D．1cm
組卷：7112引用：142難度：0.9
解析
5．一個多邊形的每個外角都等于60°，則這個多邊形的邊數為（　　）
A．8 B．7 C．6 D．5
組卷：995引用：75難度：0.7
解析
6．下列變形中，正確的是（　　）
A．-
1
a
=
-
1
a
B．
1
a
+
1
b
=
1
a
+
b
C．
2
b
2
a
2
=
2
b
a
D．
a
+
ab
b
+
ab
=
a
b
組卷：157引用：4難度：0.9
解析
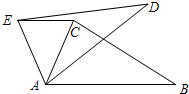7．如圖在△ABC中，∠CAB=70°，在同一平面內，將△ABC繞點A逆時針旋轉到△ADE的位置，使得EC∥AB，則∠CAE度數為（　　）
A．30° B．35° C．40° D．50°
組卷：250引用：5難度：0.7
解析
8．關于x的分式方程
2
x
-
a
x
+
1
=1的解為正數，則字母a的取值范圍為（　　）
A．a≥-1 B．a＞-1 C．a≤-1 D．a＜-1
組卷：10215引用：64難度：0.9
解析

24．某校為美化校園，計劃對面積為1800m²的區域進行綠化，安排甲、乙兩個工程隊完成．已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化的面積的2倍，并且在獨立完成面積為400m²區域的綠化時，甲隊比乙隊少用4天．
（1）求甲、乙兩工程隊每天能完成綠化的面積分別是多少m²？
（2）若學校每天需付給甲隊的綠化費用為0.4萬元，乙隊為0.25萬元，要使這次的綠化總費用不超過8萬元，至少應安排甲隊工作多少天？
組卷：12250引用：126難度：0.3
解析
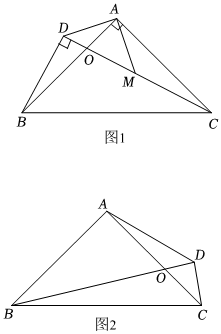25．如圖，在Rt△ABC中，∠BAC=90°，AB=AC，在BC的同側作任意Rt△DBC，∠BDC=90°．
（1）若CD=2BD，M是CD中點（如圖1），求證：AD=AM；
下面是小明的證明過程，請你將它補充完整：
證明：設AB與CD相交于點O，
∵∠BDC=90°，∠BAC=90°，
∴∠DOB+∠DBO=∠AOC+∠ACO=90°．
∵∠DOB=∠AOC，
∴∠DBO=∠
．
∵M是DC的中點，CD=2BD，
∴CM=
1
2
CD=
．
又∵AB=AC，
∴△ADB≌△AMC．
∴AD=AM．
（2）若CD＜BD（如圖2），在BD上是否存在一點N，使得△ADN是以DN為斜邊的等腰直角三角形？若存在，請在圖2中確定點N的位置，并加以證明；若不存在，請說明理由；
（3）當CD≠BD時，線段AD，BD與CD滿足怎樣的數量關系？請直接寫出．
組卷：40引用：1難度：0.3
解析