用反證法證明“a<|a|”,求證:a必為負數.
證明:假設a不是負數,那么a是正數正數或a是零零.
(1)如果a是零,那么a=|a|,這與題設矛盾,所以a不可能是零;
(2)如果a是正數正數,那么a=|a|,這與題設題設矛盾,所以a不可能是正數正數.
綜合(1)和(2),知a不可能是正數正數,也不可能是零零.所以a必為負數.
【答案】正數;零;正數;題設;正數;正數;零
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/22 18:0:1組卷:148引用:1難度:0.7
相似題
-
1.用反證法證明“三角形中最多有一個鈍角”時,第一步應假設( )
A.三角形中有一個鈍角 B.三角形中有兩個鈍角或三個鈍角 C.三角形中有一個銳角 D.三角形中有兩個銳角 發布:2025/6/22 18:30:2組卷:305引用:5難度:0.6 -
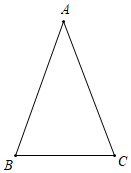 2.用反證法證明:等腰三角形的底角必定是銳角.
2.用反證法證明:等腰三角形的底角必定是銳角.
已知:在△ABC中,AB=AC.求證:∠B,∠C必為銳角.發布:2025/6/22 18:30:2組卷:429引用:5難度:0.7 -
3.要證明命題“若a>b,則a2>b2”是假命題,下列a,b的值不能作為反例的是( )
A.a=1,b=-2 B.a=0,b=-1 C.a=-1,b=-2 D.a=2,b=-1 發布:2025/6/22 19:0:1組卷:1144引用:37難度:0.9


