【了解概念】
我們知道，折線段是由兩條不在同一直線上且有公共端點的線段組成的圖形．如圖1，線段MQ、QN組成折線段MQN．若點P在折線段MQN上，MP=PQ+QN，則稱點P是折線段MQN的中點．
【理解應用】
（1）如圖2，⊙O的半徑為2，PA是⊙O的切線，A為切點，點B是折線段POA的中點．若∠APO=30°，則PB=33；
【定理證明】
（2）阿基米德折弦定理：如圖3，AB和BC是⊙O的兩條弦（即折線段ABC是圓的一條折弦），BC＞AB，點M是?ABC的中點，從M向BC作垂線，垂足為D，求證：D是折弦ABC的中點；
【變式探究】
（3）如圖4，若點M是?AC的中點，【定理證明】中的其他條件不變，則CD、DB、BA之間存在怎樣的數量關系？請直接寫出結論．
【靈活應用】
（4）如圖5，BC是⊙O的直徑，點A為⊙O上一定點，點D為⊙O上一動點，且滿足∠DAB=45°，若AB=8，BC=10，則AD=72或272或2．
?
ABC
?
AC
2
2
2
2
【考點】圓的綜合題．
【答案】3；7或
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/17 4:0:1組卷：992引用：2難度：0.3
相似題
-
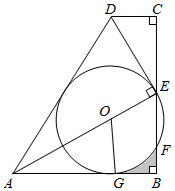1．如圖，四邊形ABCD中，∠B=∠C=90°，點E為BC中點，AE⊥DE于點E．點O是線段AE上的點，以點O為圓心，OE為半徑的⊙O與AB相切于點G，交BC于點F，連接OG．
（1）求證：△ECD∽△ABE；
（2）求證：⊙O與AD相切；
（3）若BC=6，AB=3，求⊙O的半徑和陰影部分的面積．3發布：2025/5/21 14:30:1組卷：1854引用：4難度：0.3 -
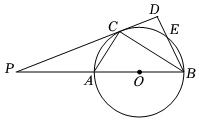2．如圖，AB是⊙O的直徑，E為⊙O上的一點，∠ABE的平分線交⊙O于點C，過點C的直線交BA的延長線于點P，交BE的延長線于點D．且∠PCA=∠CBD．
（1）求證：PC為⊙O的切線；
（2）若PC=2BO，PB=12，求⊙O的半徑及BE的長．2發布：2025/5/21 15:0:1組卷：1340引用：4難度：0.1 -
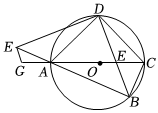3．如圖，在Rt△ABC中，∠ABC=90°，以AC為直徑作⊙O，BD平分∠ABC交⊙O于D，BD交AC于點E，過點D作DF⊥DB，DF交BA的延長線于點F，過點F作FG∥BD交CA的延長線于點G．
（1）求證：△DAF≌△DCB；
（2）如果tan∠FAG=，求13的值；DEBE
（3）寫出AG與CE的數量關系，并說明理由．發布：2025/5/21 14:30:1組卷：235引用：1難度：0.1