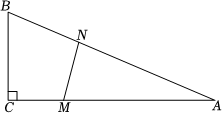
如圖，在△ABC中，∠C=90°，BC=5米，AC=12米．M點在線段CA上，從C向A運動，速度為1米/秒；同時N點在線段AB上，從A向B運動，速度為2米/秒．運動時間為t秒．
（1）當t為何值時，∠AMN=∠ANM？
（2）當t為何值時，△AMN的面積最大？并求出這個最大值；
（3）當t為何值時，△ABC與△AMN相似？
【考點】相似形綜合題．
【答案】（1）4；
（2）當t=6時，S最大值=平方米；
（3）當t=或t=時，△AMN與△ABC相似．
（2）當t=6時，S最大值=
180
13
（3）當t=
72
19
156
37
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：249引用：1難度：0.5
相似題
-
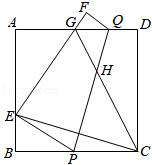1．如圖，將正方形紙片ABCD沿PQ折疊，使點C的對稱點E落在邊AB上，點D的對稱點為點F，EF交AD于點G，連接CG交PQ于點H，連接CE，EH．
（1）求證：△PBE∽△QFG；
（2）求∠ECG的度數；
（3）求證：EG2-CH2=GQ?GD．發布：2025/5/25 21:0:1組卷：400引用：2難度：0.3 -
2．問題提出
如圖（1），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，點E在△ABC內部，直線AD與BE交于點F．線段AF，BF，CF之間存在怎樣的數量關系？
問題探究
（1）先將問題特殊化如圖（2），當點D，F重合時，直接寫出一個等式，表示AF，BF，CF之間的數量關系；
（2）再探究一般情形如圖（1），當點D，F不重合時，證明（1）中的結論仍然成立．
問題拓展
如圖（3），在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC（k是常數），點E在△ABC內部，直線AD與BE交于點F．直接寫出一個等式，表示線段AF，BF，CF之間的數量關系．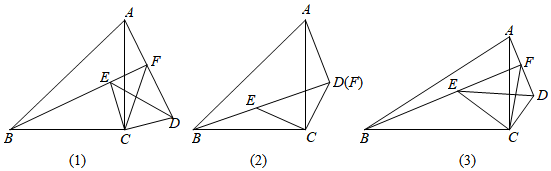
發布：2025/5/25 17:30:1組卷：5696引用：14難度：0.6 -
3．【證明體驗】（1）如圖1，△ABC中，D為BC邊上任意一點，作DE⊥AC于E，若∠CDE=
∠A，求證：△ABC為等腰三角形；12
【嘗試應用】
（2）如圖2，四邊形ABCD中，∠D=90°，AD=CD，AE平分∠BAD，∠BCD+∠EAD=180°，若DE=2，AB=6，求AE的長；
【拓展延伸】
（3）如圖3，△ABC中，點D在AB邊上滿足CD=BD，∠ACB=90°+∠B，若AC=1012，BC=20，求AD的長．3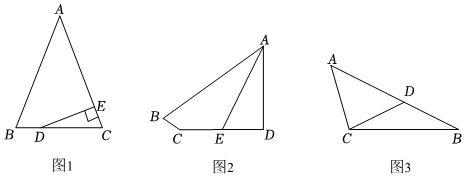
發布：2025/5/25 20:0:1組卷：497引用：1難度：0.3